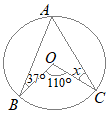
 【例題1】
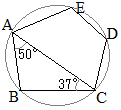
【例題1】右の図のように,円Oの周上に点A, B, Cがある。 このとき,∠xの大きさを求めなさい。 (富山県2015年入試問題)
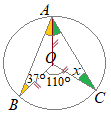 (解答)
(解答)△OCAは,二等辺三角形だから2つの底角は等しい.(右図の緑で示した角x) 同様にして,△OABも二等辺三角形だから2つの底角は等しい.(右図の黄色で示した角37°) 次に,円周角は中心角の半分だから ∠ ∠x=18°…(答) |
【要点】
一般に,高校入試問題では「円周角の定理」を覚えているだけでは,問題は解けません.この問題では,次の2つの定理を組み合わせて解いています.
(1) 二等辺三角形の2つの底角は等しい.(2) 円周角は中心角の半分になる.
特に,(1)を使って元の角xの代わりに,他の角∠BACで計算する方法が使えるようにしましょう.
|
【問題1】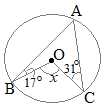 (1)
(1)右の図において,点A, B, Cは円周上の点である。∠xの大きさを求めなさい。 (栃木県2015年入試問題)
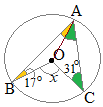 右図において,緑で示した2つの角は,二等辺三角形の底角だから等しい
右図において,緑で示した2つの角は,二等辺三角形の底角だから等しい∠OAC=31° 黄色で示した2つの角も,二等辺三角形の底角だから等しい ∠OAB=17° 円周角は中心角の半分(中心角は円周角の2倍)だから ∠x=2×(31°+17°)=96°…(答) |
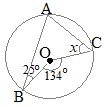 (2)
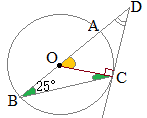
(2)右の図において,3点A, B, Cは円Oの周上の点である。∠ABO=25°, ∠BOC=134°のとき,∠xの大きさを求めなさい。 (秋田県2017年入試問題)
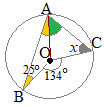 右図において,緑で示した2つの角は,二等辺三角形の底角だから等しい
右図において,緑で示した2つの角は,二等辺三角形の底角だから等しい∠OAC=∠x 黄色で示した2つの角も,二等辺三角形の底角だから等しい ∠OAB=25° 円周角は中心角の半分(中心角は円周角の2倍)だから ∠x+25=67° ∠x=42°…(答) |
 【例題2】
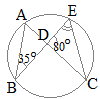
【例題2】右の図のような円があり,異なる3点A, B, Cは円周上の点である。線分AC上に,2点A, Cと異なる点Dをとる。また,2点B, Dを通る直線と円との交点のうち,点Bと異なる点をEとする。 ∠ABE=35°, ∠CDE=80°であるとき,∠BECの大きさは何度か。 (香川県2017年入試問題)
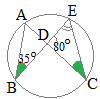 (解答)
(解答)∠ABEと∠ACEは,一つの弧 次に,三角形の内角の和は180°だから 80°+35°+∠DEC=180° ∠DEC=65°…(答) |
【要点】
一般に,高校入試問題では「円周角の定理」を覚えているだけでは,問題は解けません.この問題では,次の2つの定理を組み合わせて解いています.
(1) 一つの弧に対する円周角は等しい.(2) 三角形の内角の和は180°になる. |
【問題2】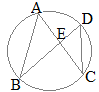 (1)
(1)右の図のように,円周上に4点A, B, C, Dがあり,線分ACと線分BDの交点をEとします。∠ACD=35°, ∠AEB=95°のとき,∠BACの大きさは何度ですか。 (広島県2017年入試問題)
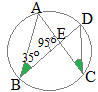 右図において,緑で示した2つの角は,一つの弧
右図において,緑で示した2つの角は,一つの弧次に,三角形の内角の和は180°だから ∠BAC+35°+95°=180° ∠BAC=50°…(答) |
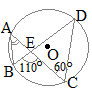 (2)
(2)右の図において,4点A, B, C, Dは円Oの周上にあり,線分AC, BDの交点をEとする。∠BEC=110°, ∠ACD=60°のとき,∠BACの大きさを求めなさい。 (山梨県2017年入試問題)
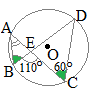 右図において,緑で示した2つの角は,一つの弧
右図において,緑で示した2つの角は,一つの弧また,∠AEBは∠BECの補角だから ∠AEB=180°−110°=70° 次に,三角形の内角の和は180°だから ∠BAC+60°+70°=180° ∠BAC=50°…(答) |
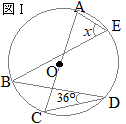 【例題3】
【例題3】右の図Ⅰにおいて,ACが円Oの直径であるとき,∠xの大きさを求めなさい。 (鳥取県2015年入試問題)
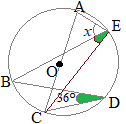 (解答)
(解答)右図のように線分CEをひくと∠CDBと∠CEBは,1つの弧
この問題では,線分ADをひいて,∠CDA=90°を利用してもよい
次に,∠CEAは,直径に対する円周角だから90°∠x+36°=90° ∠x=54°…(答) |
【要点】
直径という条件の使い方:「円周角が90°になる」 |
【問題3】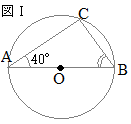 (1)
(1)右の図Ⅰのような円において,∠ABCの大きさを求めよ。 (長崎県2015年入試問題)
|
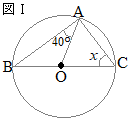 (2)
(2)図Ⅰのように,円Oの周上に3点A, B, Cがあり,BCは直径である。∠xの大きさは何度か,求めなさい。 (兵庫県2015年入試問題)
|
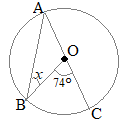 (3)
(3)右の図のように,円Oの円周上に3つの点A, B, Cがあり,∠BOC=74°であるとき,∠xの大きさを答えなさい。 (新潟県2015年入試問題)
∠COAは,中心角∠COBに対応する円周角だから,その半分になる.
∠COA=37° △OABはOA=OBの二等辺三角形だから ∠x=∠COA=37°…(答) ※この問題は,直径の円周角が90°ということを使わなくても解けます. |
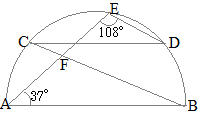 (4)
(4)右の図は,線分ABを直径とする半円で,2点C, Dは ∠BAE=37°, ∠AED=108°のとき,∠BFEの大きさを求めなさい。 (熊本県2015年入試問題)
円周角が90°という図を書けば,ABが直径という条件が使えます.
FからCDに平行な線を引けば,CD//ABという条件が使えます. 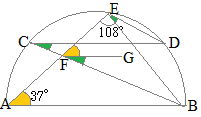 (解答)
右図のように線分BEを引くと,∠AEBは直径ABに対応する円周角だから90°.
(解答)
右図のように線分BEを引くと,∠AEBは直径ABに対応する円周角だから90°.したがって, ∠BED=18° 円周角は等しいから ∠BCD=18° 平行線の同位角は等しいから ∠BFG=18° また,平行線の同位角は等しいから ∠GFE=∠BAE=37° 以上から ∠BFE=37°+18°=55°…(答) |
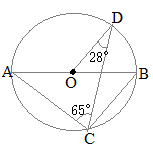 (5)
(5)右の図において,線分ABは円Oの直径であり,2点C, Dは円Oの周上の点である。 このとき,∠ABCの大きさを求めなさい。 (神奈川県2015年入試問題)
円周角が90°という図を書けば,ABが直径という条件が使えます.
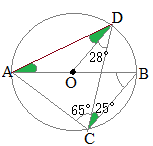 (解答)
(解答)∠ACBは直径ABに対応する円周角だから90°. したがって, ∠BCD=25° 円周角は等しいから ∠BAD=25° 二等辺三角形の2つの底角は等しいから ∠ADO=25° 求める角度∠ABCは,円周角∠ADCに等しいから ∠ABC=25°+28°=53°…(答) |
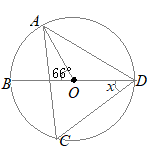 (6)
(6)右の図のように,円Oの円周上に4点A, B, C, Dがあり,線分BDは円Oの直径です。 AC=AD, ∠AOB=66°のとき,∠BDCの大きさxを求めなさい。 (埼玉県2015年入試問題)
円周角が90°という図を書けば,BDが直径という条件が使えます.
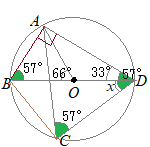 (解答)
(解答)∠ADOは中心角∠AOBに対応する円周角だから33° △ABDは直角三角形だから ∠ABD=90°−33°=57° 円周角は等しいから ∠ABD=∠ACD=57° 二等辺三角形の2つの底角は等しいから ∠ACD=∠CDA=57° ∠x=57°−33°=24°…(答) ※∠BCD=90°を使って解くこともできます. |
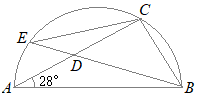 (7)
(7)右の図は,線分ABを直径とする半円で,点Cは, ∠BAD=28°であるとき,∠DCEの大きさを求めなさい。 (熊本県2017年入試問題)
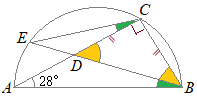 (解答)
(解答)∠ACBは直径に対応する円周角だから90° したがって ∠ABC=90°−28°=62° 次に,DC=BCだから,△DBCは直角二等辺三角形になり ∠CBD=45° ∠ABD=62°−45°=17° 弧 ∠DCE=17°…(答) |
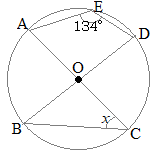 (8)
(8)右の図のように,円Oの円周上に5つの点A, B, C, D, Eがあり,線分ACとBDは円の中心Oで交わっている。∠AED=134°であるとき,∠xの大きさを答えなさい。 (新潟県2017年入試問題)
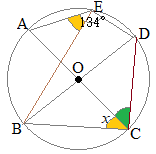 (解答)
(解答)∠AEDと∠ACDとは円に内接する四角形の向かい合う角だからそれらの和は180° ∠ACD=180°−134°=46° ∠BCDは直径に対応する円周角だから90° ∠x=90°−46°=44°…(答) (別解) ∠BEDは直径に対応する円周角だから90° ∠AEB=134°−90°=44° 同一の弧 ∠ACB=∠AEB=44°…(答) ※この問題を解く上で,BDが直径であることは重要であるが,ACが直径であることは使わなくても解ける. |
【問題4】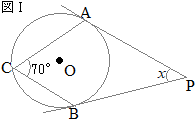 (1)
(1)右の図Ⅰにおいて,∠xの大きさを求めなさい。ただし,PA, PBは円Oの接線で,点A, Bはその接点である。また,点Cは円Oの周上の点である。 (鳥取県2017年入試問題)
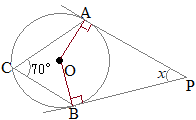 ∠AOBは∠ACBに対する中心角だから
∠AOBは∠ACBに対する中心角だから∠AOB=140° OA⊥AP, OB⊥BPであり,四角形の内角の和が360°になることから 140°+90°+90°+∠x=360° ∠x=40°…(答) |
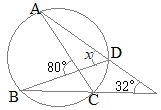 (2)
(2)右の図のように,円周上に4点A, B, C, Dがあるとき,x=°である。 (岡山県2015年入試問題)
 対頂角は等しいから
対頂角は等しいから∠DEC=80° 円周角は等しいから ∠ECB=∠x このxを用いて,四角形DECFの内角の和を求めると 80°+180°−∠x+180°−∠x+32°=360° 2∠x=112° ∠x=56°…(答) |
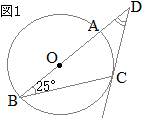 (3)
(3)図1のような円Oにおいて,線分ABは円Oの直径である。円Oの周上の点Cを通る接線と直線ABとの交点をDとする。∠ABC=25°のとき,∠BDCの大きさを求めよ。 (長崎県2017年入試問題)
|
 半径OCは接線CDと垂直
半径OCは接線CDと垂直∠OCD=90° △OBCは二等辺三角形だから ∠BCO=25° △OBCの2つの内角の和は,1つの外角に等しいから ∠AOC=25°+25°=50° △OCDの内角の和は180°だから ∠BDC=40°…(答) |
【問題5】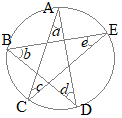 (1)
(1)右の図で,∠a+∠b+∠c+∠d+∠eの大きさを求めなさい。 |
(2)
右の図で,∠a+∠b+∠c+∠d+∠e+∠f+∠gの大きさを求めなさい。 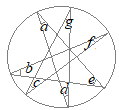 (山梨県2015年入試問題)
|
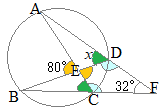
 (3)
(3)右の図のように,円に内接する五角形ABCDEがある。∠BAC=50°, ∠ACB=37°, AB=CDのとき,∠AEDの大きさを求めなさい。 (新潟県2000年入試問題)
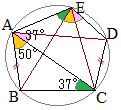 まず,AB=CDから,弦の長さが等しいとき円周角は等しくなるから
まず,AB=CDから,弦の長さが等しいとき円周角は等しくなるから∠CAD=37° 次に,緑色,黄色,桃色の角度はそれぞれ円周角として等しい ∠BAC=∠BEC, ∠ACB=∠AEB, ∠CAD=∠CED, したがって ∠AED=37°+37°+50°=124°…(答) |
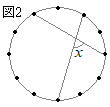 (4)
(4)図2で,円周上の12点は円周を12等分している。∠xの大きさを求めよ。 (奈良県2000年入試問題)
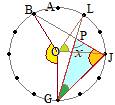 ∠x自体は円周角ではないので,直接は求められませんが,三角形の残りの角が円周角として求まると,∠xを間接的に求めることができます.
∠x自体は円周角ではないので,直接は求められませんが,三角形の残りの角が円周角として求まると,∠xを間接的に求めることができます.例えば,右図の1つの三角形△PGJにおいて,円周角∠LGJに対応する中心角∠LOJ=60°だから ∠LGJ=30° また,円周角∠BJGに対応する中心角∠BOG=150°だから ∠BJG=75° 次に,三角形△PGJの内角の和は180°だから ∠x+30°+75°=180° したがって ∠x=75°…(答) |
|
※参考・・・角度を表す記号の書き方 中学校数学の教科書10冊を見て,角度を表す記号がどのように使われているか調べた. 1. まず,角度を表す定数は,図の中でも,文章や式の中でも,30°などと書き,∠30°,30などと書かれることはない.これについては,すべての教科書で一致している. 2. 次に,角度を表す未知数xの書き方は,次のように分かれる.
①「図の中ではxと書き,文章や式の中では「角x」または「∠x」などと書くもの
(同一の出版社が複数の教科書を出している場合,添え字で区別)
K社1,K社2,K社3,T社1,T社2,O社の6社
② (A)「図の中ではxと書き,文章や式の中では「角x」または「∠x」などと書く方法と
(B)「図の中ではx°と書き,文章や式の中では「角x」または「x」などと書く方法 を併用しているもの
(同一の出版社が複数の教科書を出している場合,添え字で区別)
T社,G社,S社,D社の4社 |
③ 高校では「図の中ではxと書き,文章や式の中でもxなどと書くことが多い.1年後にこうなるので,違いの正誤をあまり頑張っても,得られることが少ない.(∠ABCなどは,∠の記号を使う.)
以上の集計から,①の「図の中ではxと書き,文章や式の中では「角x」または「∠x」などと書くのが多数派のようなので,この教材でもそれにそろえた.ただし,2015年埼玉県,岡山県の入試問題は,著作権が当該教育委員会にあり,当教材は公開されている出版物の引用という立場なので,問題を改変することはできない.解説・解答のみ書き換えることができる.
例えば正弦定理は,例外なく次のように書き,「sin∠A」などはめったに書かない.
中高一貫の場合,中高で重複しやすい内容は1回で教えるから,高校と同じく,図の中でも,式の中でも単にxと書く場合が多いと想像できる.
|
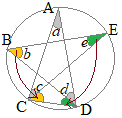 右図のように,円周角が等しいことを使って,緑色,黄色の角度
右図のように,円周角が等しいことを使って,緑色,黄色の角度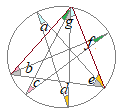 右図のように,円周角が等しいことを使って,緑色,黄色,水色,桃色の角度
右図のように,円周角が等しいことを使って,緑色,黄色,水色,桃色の角度