|
2a , −3xy2のように、数や文字についての乗法だけで作られている式を単項式といいます。 5 , xのように、1つの数や1つの文字だけのものも単項式といいます。
【例】
2a , ab , 3a2 , −7 , xは単項式です。 ■ 単項式の係数と次数 単項式の数の部分を係数といいます。ただし、1xのように係数が1のときは省略してxと表されるので、xの係数は1です。同様にして、−1aのように係数が−1のときは省略して−aと表されるので、−aの係数は−1です。
【例】
単項式で掛けられている文字の個数をその単項式の次数といいます。文字の部分ではなく、文字の個数が次数であることに注意しましょう。
2a → 係数は2 −3xy2 → 係数は−3 x → 係数は1
【例】
x2や−4x3のように累乗の形で表されているときは、指数の部分(右上に付いている小さな数)が文字の個数、すなわち次数を表します。ただし、xのように指数が付いていない式はx0ではなくx1を表します。
2a → 次数は1 −3xy → 次数は2
【例】
x2y3や2ab2のように文字で表されている変数が2種類以上あるとき、単項式の次数、すなわち、掛けられている文字の個数は各々の指数の和になります。
5a4 → 次数は4 −3x2 → 次数は2 2x → 次数は1
【例】
4a2b3 → 次数は2+3=5 −3xy2 → 次数は1+2=3 ■ 定数項 数の部分だけから成り立っている単項式は定数項と呼ばれます。定数項の係数はその数自体、定数項の次数は0です。
【例】
5 → 係数は5、次数は0 −7 → 係数は−7、次数は0 ※数学では用語の使い方は定義によって決まります。中学生向けの教材の中では、「文字に掛けられている数を係数」と教えている場合があります。その立場の教材では、「定数項には文字がないから、係数は考えない」と教えることがあるようです。(中学の教科書(大手3社)で文字がないときの係数を扱っている例は見当たりませんが、係数を使うときは必ず定数項以外について尋ねています。)
 |
※ 「乗法だけで作られている式」という限定によって、単項式は加法や減法を含む多項式から区別されます。
3xは単項式
x+3 , 2x−5は単項式ではなく、多項式 さらに、「乗法だけ」という限定によって、単項式は文字(変数)の部分が割り算になっている分数式などと区別されます。
3xは単項式
は単項式ではなく、分数式と呼ばれる。 ただし、数字の部分が分数になっているもの、例えばxは、小数の形0.25xで表すことができることから分かるように、「分数(小数)という数が掛けられたもの」と見なせるので、単項式です。
xすなわち0.333…xは単項式
文字で割ってあるもの: → 単項式ではない
数字で割ってあるもの:x=0.5x → 単項式 |
|
■ 多項式 2a+b , 3x−4yのように単項式の和の形で表される式を多項式といいます。(3x−4yは3x+(−4y)と書くことができ、−4yの係数は−4です。) 多項式を構成しているそれぞれの単項式を項といいます。
【例】
2a+3は多項式、2a , 3は項 x2−3x+5は多項式、x2 , −3x , 5は項 ■ 降べきの順 変数(文字)が1種類である多項式を分かりやすく並べるときに、各項の次数の高いものから低いものへ並べる方法を降べきの順といいます。中学、高校では、ほとんどの場合に多項式は降べきの順に整理します。
【例】
3x−4+5x2を降べきの順に整理すると5x2+3x−4 ※2文字以上あるときは、降べきの順ということだけでは順序が決まらないことがあります。 a2+2ab+3b2 → どれも2次なので書き方は自由 ※高校では、1+x+x2+···+xn+···のように項の数が無限にあるような場合は、次数の低い項から順に並べます。これを昇べきの順といいます。(降べきの順に書こうとすると「書き始めることができない」) ■ 多項式の次数 多項式の次数は各項の次数のうちで「最も高い次数」とします。
(注意:よくある間違い)単項式の次数は「掛けられている文字の個数」で、2種類以上の文字が含まれているとき、単項式の次数は「各々の指数の和」でしたが、多項式の次数は次数の「最も高い項」だけで決めます。
【例】
単項式では:4a2b3 → 次数は2+3=5 多項式では:x2+3x+4 → 次数は2(2次式という) (よくある間違い:3次)
多項式では:x3+x2+x+1 → 次数は3(3次式という)(よくある間違い:6次)
多項式では:x2+3xy−x+3 → 次数は2(2次式という)※2次が2つあるとき高い方は2次とする。(同順なら2つとも最高)
次数の低い項は「多項式の次数に無関係」
次数の低い項の顔を立てる必要なし:「面目丸つぶれ」でよい。 |
※「降べきの順、昇べきの順」に登場する「べき」という言葉は、累乗のことを表しています。
a , a2 , a3 , ···をaの「べき」といいます。
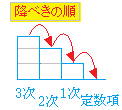
降べきの順とは、累乗の指数の高いものから低いものへと階段を降りるように並べることを表しています。
問題3 次の各式について単項式であるか、多項式であるか、いずれでもないか答えてください。
(英語で単項式はmonomial、多項式はpolynomialといいます。各々前の空欄に、単項式なら m を、多項式なら p を、どちらでもないなら n を小文字で記入してください。) |