|
多角形の外角
よくある間違い:図１のように、多角形の１つの辺とこれに隣接する辺の延長とがなす角を外角という. 外角は内角の補角である. 外角は図２のような角ではない. 注意: 各内角には２つの外角があるが,外角の大きさというときにはそのうちの１つだけを指す. |
図 1
   |
||||||||||||||||||
|
多角形の外角の和
多角形の外角の和は360°である.
(証明)外角を辺に沿って集めると,１点の周りの角になる. １点のまわりの角は360°であるから,外角の和は360°になる. |
(クリック)→集める (クリック)→外角に分ける 図 4  |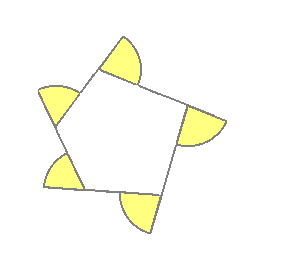
||||||||||||||||||
|
ｎ角形の内角の和
ｎ角形の内角の和は180°×(n−2).
(証明 1)ｎ角形の頂点の個数はｎ個である. (図5) ｎ個の内角とｎ個の外角の総和は, |
図5
 |
||||||||||||||||||
|
(証明 2) １つの三角形の内角の和は180°. 図6で示されるように, ｎ角形はn−2個の三角形に分けられるから,内角の和は(n−2)×180°. |
 |
||||||||||||||||||
問題 1
1.xの大きさを求めなさい.
|
(外角)=180°−110°=70° | ||||||||||||||||||
2.xの大きさを求めなさい.
|
三角形の内角の和は180°だから50°+30°+∠a=180° ∠a=100° 内角と外角の和は180°. ∠x=180°−∠a=180°−100°=80° |
||||||||||||||||||
3.x+y+zの大きさを求めなさい.
|
三角形の内角の和は180°だから∠a+∠b+∠c=180° 各々の内角,外角の組は対頂角だから等しい. ∠x=∠a ∠y=∠b ∠z=∠c ゆえに, ∠x+∠y+∠z=∠a+∠b+∠c=180° |
||||||||||||||||||
4.xの大きさを求めなさい.
|
外角の和は360°だから 70°+110°+∠x+120°=360° ゆえに, ∠x=60° |
||||||||||||||||||
5.xの大きさを求めなさい.
|
５角形の内角の和は180°×3=540°. 120°+80°+110°+95°+∠x=540° ゆえに, ∠x=135° |
||||||||||||||||||
|
正多角形
すべての辺の長さが等しく,すべての内角の大きさが等しい多角形を正多角形という.
(証明)正多角形の１つの外角の大きさは 正多角形の１つの内角の大きさは 180°− •多角形の外角の和は360°. 正多角形のすべての内角の大きさは等しく,すべての外角の大きさは等しい. したがって,正ｎ角形の１つの外角の大きさは •(内角)=180°−(外角) したがって,正ｎ角形の１つの内角は 180°−
(別の証明)
多角形の内角の和は 180°×(n−2). 正多角形のすべての内角の大きさは等しいから,正ｎ角形の１つの内角の大きさは =180°− |
例 • 正三角形外角= =120° 内角=180°−120° =60°  • 正方形外角= =90° 内角=180°−90° =90°  • 正五角形外角= =72° 内角=180°−72° =108° |
||||||||||||||||||
問題 2
1.xの大きさを求めなさい.
|
正六角形の１つの内角の大きさは 180°−=120° |
||||||||||||||||||
2.xの大きさを求めなさい.
|
正八角形の１つの内角の大きさは 180°−=135° |
||||||||||||||||||
3.xの大きさを求めなさい.
|
正十角形の外角の大きさは =36° |