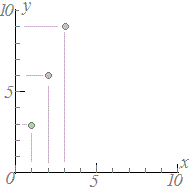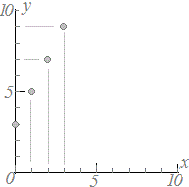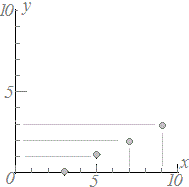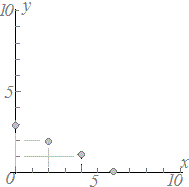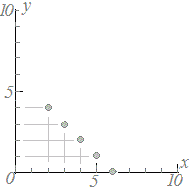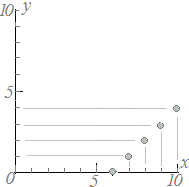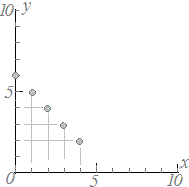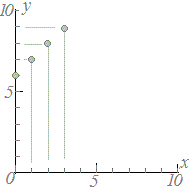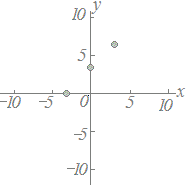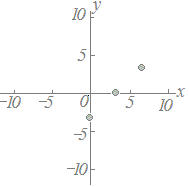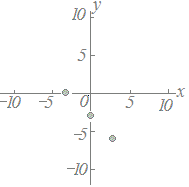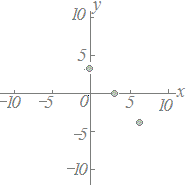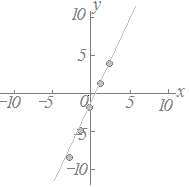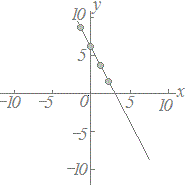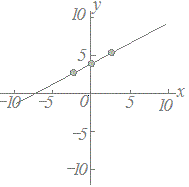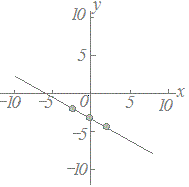|
迴ｾ蝨ｨ蝨ｰ縺ｨ蜑榊ｾ後�鬆�岼 *** 螟牙喧縺ｮ蜑ｲ蜷� ***/螟牙喧縺ｮ蜑ｲ蜷�1/螟牙喧縺ｮ蜑ｲ蜷�2/螟牙喧縺ｮ蜑ｲ蜷�3/髢｢謨ｰ縺ｮ蛟､縺ｨ螟牙喧縺ｮ蜑ｲ蜷�/*** 蛯ｾ縺阪→蛻�援 ***/荳谺｡髢｢謨ｰ�亥だ縺阪∝�迚�ｼ�/轤ｹ縲∝だ縺坂�逶ｴ邱壹�蠑�/荳谺｡髢｢謨ｰ縺ｮ繝��繧ｿ縺ｨ繧ｰ繝ｩ繝�/繧ｰ繝ｩ繝補�蛯ｾ縺�,蛻�援/螻暮幕蠖｢竊貞だ縺搾ｼ悟�迚�/髢｢菫ょｼ�/*** 逶ｴ邱壹�繧ｰ繝ｩ繝� ***/繧ｰ繝ｩ繝補�逶ｴ邱壹�蠑�1/繧ｰ繝ｩ繝補�逶ｴ邱壹�蠑�2/繧ｰ繝ｩ繝補�逶ｴ邱壹�蠑�3/繧ｰ繝ｩ繝補�逶ｴ邱壹�蠑�4/繧ｰ繝ｩ繝補�逶ｴ邱壹�蠑�5/譁ｹ遞句ｼ鞘�蛻�援縺ｨ蛯ｾ縺�1/譁ｹ遞句ｼ擾ｼ亥ｱ暮幕蠖｢�俄�蛻�援縺ｨ蛯ｾ縺�2/譁ｹ遞句ｼ鞘�轤ｹ3/譁ｹ遞句ｼ鞘�蛻�援/逶ｴ邱壹�蛯ｾ縺�/螻暮幕蠖｢竊貞�迚�/譁ｹ遞句ｼ鞘�繧ｰ繝ｩ繝�4/譁ｹ遞句ｼ鞘�繧ｰ繝ｩ繝�5/*** 蟷ｳ陦後↑�堤峩邱� ***/蟷ｳ陦後↑�堤峩邱壹ｒ縺輔′縺�1/蟷ｳ陦後↑�堤峩邱壹ｒ縺輔′縺�2/蟷ｳ陦後↑�堤峩邱壹ｒ縺輔′縺�3/逶ｴ邱壹�蟷ｳ陦檎ｧｻ蜍�1/逶ｴ邱壹�蟷ｳ陦檎ｧｻ蜍�2/*** 騾壹ｋ繝ｻ騾壹ｉ縺ｪ縺� ***/騾壹ｋ/騾壹ｉ縺ｪ縺�/騾｣遶区婿遞句ｼ上→繧ｰ繝ｩ繝�/縺ゅｋ繝ｻ縺ｪ縺�け繧､繧ｺ/*** 髱｢遨� ***/蝗ｳ蠖｢縺ｮ髱｢遨�1/蝗ｳ蠖｢縺ｮ髱｢遨�2/*** �堤せ繧帝壹ｋ逶ｴ邱� ***/�堤せ繧帝壹ｋ逶ｴ邱壹�譁ｹ遞句ｼ�1/�堤せ繧帝壹ｋ逶ｴ邱壹�譁ｹ遞句ｼ�2/譁�ｭ嶺ｿよ焚繧貞性繧譁ｹ遞句ｼ�1/譁�ｭ嶺ｿよ焚繧貞性繧譁ｹ遞句ｼ�2/*** 縺ｾ縺ｨ繧√→蠢懃畑蝠城｡� ***/荳谺｡髢｢謨ｰ(縺ｾ縺ｨ繧�)/荳谺｡髢｢謨ｰ縺ｮ譁�ｫ�鬘�/荳芽ｧ貞ｽ｢縺ｮ遲臥ｩ榊､牙ｽ｢/荳芽ｧ貞ｽ｢縺ｮ髱｢遨阪�莠檎ｭ牙�邱�/逶ｴ邱壹�蛯ｾ縺�(蠢懃畑蝠城｡�)/ == 一次関数のデータとグラフ == ■グラフの書き方 ○ 次の表１は右図1のように「ばねばかり」に重りを下げたときの、重りの重さ（g）とばねの長さ（cm）を表にしたものとします。
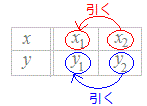
○ このような、観察・実験の結果を点のグラフで表すには、表の上の段の数字を横（x）とし、表の下の段の数字を縦（y）とする座標(x , y)を考えて点で表します。 縦に並んだ１組がx座標とy座標です。  この表にはデータが４組ありますので、図２のように点が４個できることになります。 |
図１  |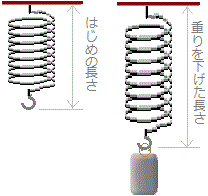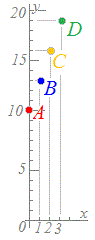
||||||||||||||||||||||||||||||
|
≪問題１≫ 次の各表において上の段の数字を横（x）に、表の下の段の数字を縦（y）として点で表したグラフを選んでください。
(1)
(2)
(3)
|
|||||||||||||||||||||||||||||||
|
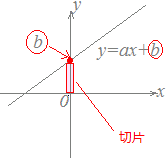
■一次関数の切片 一次関数y=ax+bにおいてbを切片といいます。 「切片」という言葉には「切り取られた断片」という意味合いが含まれており、下図の桃色で示した断片のことですが、数学では符号も付けてy座標と考えます。
|
例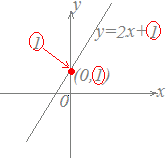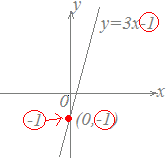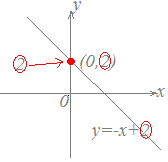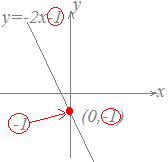   
|
||||||||||||||||||||||||||||||
|
≪問題２≫ 次の表のデータを一次関数のグラフで表したとき、直線の切片を求めてください。 |
|
||||||||||||||||||||||||||||||
|
■一次関数の傾き 一次関数y=ax+bにおいてaを傾きといいます。
|
例１
(1) x座標の差とy座標の差を考えます。 ⇒ 2−1=1と8−5=3です。 （この表では、座標が３組ありますが、必ず２組を選んで計算します。一次関数では「他の組で計算しても「分数にしたとき」同じ値になります」。） (2) 分母をx座標の差として、分子をy座標の差として計算します。 傾きは ⇒  8−52−1 = 31 = 3(3) 分母も分子もx座標やy座標ではなく、x座標の差とy座標の差です。 ⇒ 51ではありません。
(4) 右図のように、「右上がり」のグラフだから「傾きがプラス」になっていることを確かめておきます。⇒ 傾きは3 …（答）
※ x=3 , y=11の値はどうなっているのか、気になる人へ：
(1)に述べたように、この表に座標が３組ありますが、「他の組で計算しても同じ値になります」。 もし、２組の座標としてx=1 , y=5とx=3 , y=11を選んだとすると、 傾きは ⇒ 11−53−1 = 62 = 3となって、同じ結果が得られます。 ※ 分母と分子を計算するときに「引き算の順序」に注意しましょう。高校生でも上の計算が 5−81−2 = −3−1 = 3 …(*)となってしまう生徒がかなりいます。 引き算の順序を逆にしたとき、分数の値としての傾きは合っているので、途中の考え方が間違っているのを見逃しがちです。
このような生徒は見かけの向きに引きずられて（前の値）−（後の値）としてしまうようですが、例えば、1から2になったときに1−2=−1増えたなどとは言わず、2−1=1増えたと言うのが正しい。
このように「増加量」を求めるには としなければなりません。 間違って覚えてると、(*)のように傾きの計算では(−)÷(−)でも、たまたま結果が合いますが、基本的なことを問われるとバレてしまいます。 例えば「増加量」を問われると符号が逆になります。（ここで逆に覚えてしまうと、高校で登場するベクトル、複素数、定積分など広い分野で間違うことになります。） |
||||||||||||||||||||||||||||||
|
≪問題３≫ 次の表のデータを一次関数のグラフで表したとき、直線の傾きを求めてください。 |
|
||||||||||||||||||||||||||||||
