← PC用は別頁
|
≪要点≫
１次関数y=ax+bのグラフの傾きはa，切片はbです．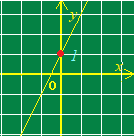 
(1) 切片は，y軸との交点（のy座標）という「目に見えるもの」なので，切片の意味を間違う生徒は少ないです．
右の図はy=2x+1の直線のグラフで，その切片は赤丸で示したy軸との交点のy座標，1です．
(2) これに対して傾きは，y=…の形に書いたときのxの係数ですが，その図形的な意味が分からない生徒が多い．
【例1】
原点(0, 0)を通り，傾きが2の直線 y=2x を図示してください．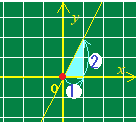 
（解答）直線の傾きは，右図のように階段状に切り出したときの，縦の長さと横の長さの比，すなわち 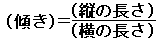 そこで，「傾きが2」の直線を描くためには「右に１だけ進んでから，上に２だけ進みます」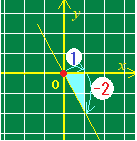 
これに対して，y=−2x のように「傾きがマイナス」の直線を描くには，「右に１だけ進んでから，下に２だけ進みます」 このように，「横の長さ」を１にすると， （傾き）＝（縦の長さ）［符号あり］になります．
【要点１】
傾きがa（符号付き）の直線を描くには， ア）傾きaの符号が正のとき
例えばa=2のとき，「右に１進んでから，上に2進む」
イ）傾きaの符号が負のとき
例えばa=−2のとき，「右に１進んでから，下に2進む」
|
|
【例2】
切片が2で，傾きが を図示してください． 
（解答）傾きが 直線の傾きは，右図のように階段状に切り出したときの，縦の長さと横の長さの比，すなわち この問題のように傾きが分数になっている場合は，「右に３進んで上に２進めばよい」． もちろん，
【要点２】
傾きが ア）傾きの符号が正のとき，
例えば
イ）傾きの符号が負のとき
例えば
|
|
【問題１】
次の２段階に分けて，１次関数 (1) 初めに，y軸上で「切片」の場所をクリックしてください．
(2) 傾きが2になるように，もう１つの点をクリックしてください．
 ，不正解：
|
|
...メニューに戻る
| 鬮ｫ�ｨ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ鬩搾ｽｵ�ｽ�ｺ鬮ｦ�ｮ陷ｻ�ｻ�ｽ�ｿ�ｽ�ｽ鬩幢ｽ｢�ｽ�ｧ�ｽ�ｽ�ｽ�ｵ鬩幢ｽ｢�ｽ�ｧ�ｽ�ｽ�ｽ�､鬩幢ｽ｢隴乗��ｽ�ｺ�ｽ�･�ｽ�ｽ�ｽ�ｽ鬩搾ｽｵ�ｽ�ｺ�ｽ�ｽ�ｽ�ｮGoogle鬮ｫ�ｶ�つ髫ｲ蟷｢�ｿ�ｽ�ｽ�ｽ�ｽ�ｴ�ｽ�ｽ�ｽ�｢鬮ｫ�ｨ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ |