【解説】(問題は下にあります.)
■ 書く順序だけを変えても、式の値は変わりませんので
(−a+b)=(b−a)・・・(1)です.
■ 引き算の順序を変えると符号が逆になりますので
(b−a)=−(a−b)・・・(2)です.
これらを使って、次のような展開ができます.
(例1)
(p+q)(−p+q)
← (1)を使う
=(p+q)(q−p)
←
p+q=q+p
を使う
=(q+p)(q−p)
←
(a+b)(a−b)=a2−b2
を使う
=q2−p2
・・・(答)
方法は一つとは限りません.(例1と同じ式について)
(p+q)(−p+q)
← (2)を使う
=−(p+q)(p−q)
←
(a+b)(a−b)=a2−b2
を使う
=−(p2−q2)
← (2)を使う
=q2−p2
・・・(答)
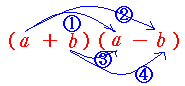 のように、とにかくバラバラにしてもできますが、 のように、とにかくバラバラにしてもできますが、
その練習だけでは、元に戻す(=次に出てくる因数分解)見通しが立たな
くなります。
ここでは、なるべく公式を用いて展開する練習をします。
【問題】
次の式を展開しなさい.(正しい式をマウスで選びなさい.)
| (1) |
(3+2x)(2x−3)
|
|
|
=
|
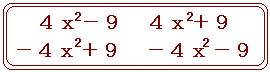 |
 |
| (2) |
(y+2)(2−y)
|
|
|
=
|
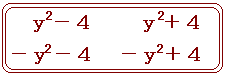 |
 |
| (3) |
(−x−7)(x−7)
|
|
|
=
|
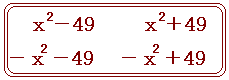 |
 |
| (4) |
(−4a+3b)(4a+3b)
|
|
|
=
|
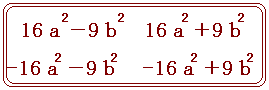 |
 |
| (5) |
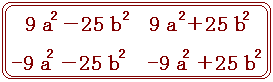
(- 3a+5b)(−3a−5b)
|
|
|
=
|
 |
 |
|
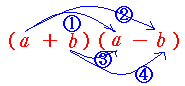 のように、とにかくバラバラにしてもできますが、
のように、とにかくバラバラにしてもできますが、
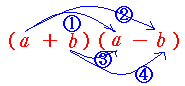 のように、とにかくバラバラにしてもできますが、
のように、とにかくバラバラにしてもできますが、