|
現在地と前後の項目 *** 変化の割合 ***/変化の割合1/変化の割合2/変化の割合3/関数の値と変化の割合/*** 傾きと切片 ***/一次関数（傾き、切片）/点、傾き→直線の式/一次関数のデータとグラフ/グラフ→傾き,切片/展開形→傾き，切片/関係式/*** 直線のグラフ ***/グラフ→直線の式1/グラフ→直線の式2/グラフ→直線の式3/グラフ→直線の式4/グラフ→直線の式5/方程式→切片と傾き1/方程式（展開形）→切片と傾き2/方程式→点3/方程式→切片/直線の傾き/展開形→切片/方程式→グラフ4/方程式→グラフ5/*** 平行な２直線 ***/平行な２直線をさがす1/平行な２直線をさがす2/平行な２直線をさがす3/直線の平行移動1/直線の平行移動2/*** 通る・通らない ***/通る/通らない/連立方程式とグラフ/ある・ないクイズ/*** 面積 ***/図形の面積1/図形の面積2/*** ２点を通る直線 ***/２点を通る直線の方程式1/２点を通る直線の方程式2/文字係数を含む方程式1/文字係数を含む方程式2/*** まとめと応用問題 ***/一次関数(まとめ)/一次関数の文章題/三角形の等積変形/三角形の面積の二等分線/直線の傾き(応用問題)/
≪要点1≫
１次関数y=ax+bのグラフは，y=axのグラフをy軸方向にbだけ平行移動させた直線になります． このグラフでは，x=0のときy=bになります．すなわち，y軸上の点(0, b)を通ります． このbの値を１次関数y=ax+bのグラフの「切片」といいます．
【例1】
次の１次関数の切片を求めてください． y=2x+3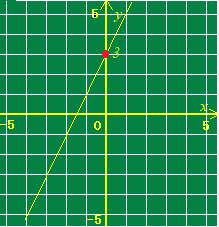 
（解答）切片は3…(答) （右図の赤丸のｙ座標） |
≪要点2≫
展開形で書かれた１次関数ax+by+c=0の切片と傾きを求めるには，yについて解かれた形（y=...の形）に直して，xの係数（傾き）と定数項（切片）を読み取ります． 傾きは
【例2】
次の１次関数の切片を求めてください． 3x+2y+6=0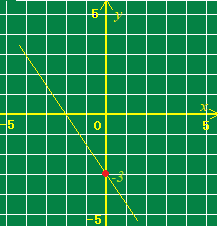 
（解答）2y=−3x−6 切片は−3…(答) （右図の赤丸のｙ座標） |
，不正解：
...メニューに戻る