|
== ��ՂȂǂ̖ڈ� ==
�s�l�����t �@�@���F�Ղ����C�����F���ʁC�������F��� �s�v�Z�ʁt �@�@���F���Ȃ��C�����F���ʁC�������F����
�m1�n
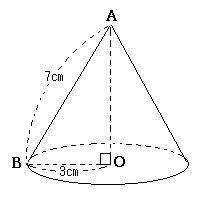 �@�E�̐}�̂悤�ȁC��ʂ��_O�𒆐S�Ƃ���~�ŁC�_A�_�Ƃ���~
�@�E�̐}�̂悤�ȁC��ʂ��_O�𒆐S�Ƃ���~�ŁC�_A�_�Ƃ���~�i2021�N ���R���������Z�������j
������������
�y�~���̑̐ρz==[�l����]���F�Ղ���,[�v�Z��]���F���Ȃ�==
��ʂ̔��a��r�C�~���̍�����h�̂Ƃ��C�~���̑̐�V�́C���̌����ŋ��߂���D�i���̌����͊o���܂��j \(\displaystyle V=\frac{1}{3}\pi r^2h\) ���̌����𗘗p���邽�߂ɁC���炩���߉~���̍���h�p�O�p�`OAB�ɂ��āC�O�����̒藝���g���ċ��߂Ă����܂��D \(\displaystyle h^2+3^2=7^2\) \(\displaystyle h=\sqrt{40}=2\sqrt{10}\) ����h�������ɑ������� \(\displaystyle V=\frac{1}{3}\pi\times 3^2\times 2\sqrt{10}=6\sqrt{10}\pi(cm^3)\)����i���j |
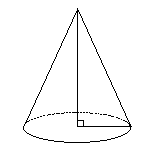 �m2�n
�m2�n�@�E�̐}�́C��ʂ̔��a�� \(3 cm\) �C���ʐς� \(24\pi cm^2\) �̉~���ł���B���̉~���̑̐ς����߂Ȃ����B�������C\(\pi\)�͉~�����Ƃ���B �i2022�N �H�c���������Z�������j
������������
==[�l����]�����F����,[�v�Z��]�����F����==
��ʂ̔��a��r�C�~���̍�����h�̂Ƃ��C�~���̑̐�V�́C���̌����ŋ��߂���D�i���̌����͊o���܂��j \(\displaystyle V=\frac{1}{3}\pi r^2h\)����@ ��ʂ̉~���̒�����L�C�~���̕���̒�����l�C�~���̑��ʂ�W�J���Ăł����`�̒��S�p��θ�Ƃ���� ��ʂ̉~���̒����́C���ʂ̐�`�̌ʂ̒����ɓ��������� \(\displaystyle 2\pi l\times\frac{\theta}{360}=2\pi\times 3\)����A �~���̑��ʐς����ʐς� \(24\pi\)������ \(\displaystyle \pi l^2\times\frac{\theta}{360}=24\pi\)����B ��ʂ̔��a3,����̒���l,�~���̍���h�͒��p�O�p�`��3�ӂ̒���������  θ�̏����ɈӊO�Ɏ肱����I θ�̏����ɈӊO�Ɏ肱����I
�B���A��θ������ \(\displaystyle l=8\) ������C�ɑ�� \(\displaystyle h^2+3^2=8^2\) \(\displaystyle h^2=64-9=55\) \(\displaystyle h=\sqrt{55}\) �@�ɑ�� \(\displaystyle V=\frac{1}{3}\pi\times 3^2\times\sqrt{55}=3\sqrt{55}\pi\hspace{5px}(cm^3)\)����i���j |
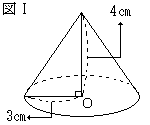 �m3�n
�m3�n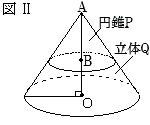 (2)�@�}�U�́C�}�T�ɂ����āC�~���̒��_��
(2)�@�}�U�́C�}�T�ɂ����āC�~���̒��_��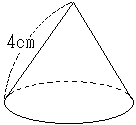 �m4�n
�m4�n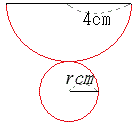 ��ʂ̔��a�̒�����
��ʂ̔��a�̒����� �m5�n
�m5�n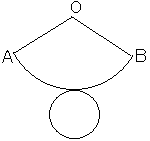 �m6�n
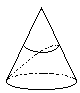
�m6�n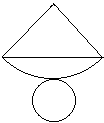 �m7�n
�m7�n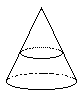
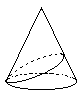
 �y�W�J�}��̒����z
�y�W�J�}��̒����z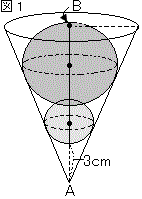 �m8�n
�m8�n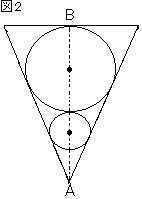 �@�܂��C�}�Q�́C�}�P�𐳖ʂ��猩���}�ł���B
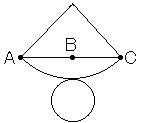
�@�܂��C�}�Q�́C�}�P�𐳖ʂ��猩���}�ł���B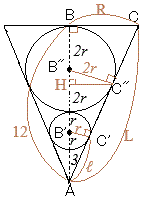 �y�~���ɐڂ��鋅�z
�y�~���ɐڂ��鋅�z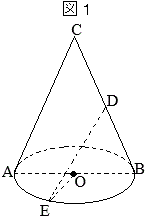 �m9�n
�m9�n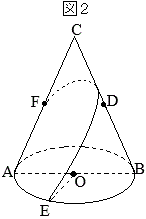 �i�E�j�@�����̒��́u���v�u���v�ɂ��Ă͂܂鐔�������ꂼ�� 0�`9 �̒�����P���I�сC���̐������Ȃ����B
�i�E�j�@�����̒��́u���v�u���v�ɂ��Ă͂܂鐔�������ꂼ�� 0�`9 �̒�����P���I�сC���̐������Ȃ����B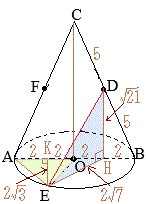
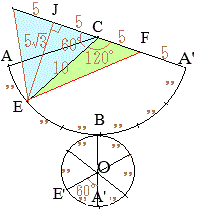 �y���n��=�W�J�}��̍ŒZ�����z
�y���n��=�W�J�}��̍ŒZ�����z �h�q���[�C���̖���10�����炢�ʼn����Ȃ�������?!
�h�q���[�C���̖���10�����炢�ʼn����Ȃ�������?!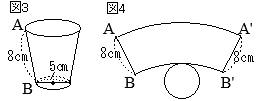
 ���͂₳�������C�w
���͂₳�������C�w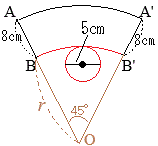 �E�̓W�J�}�ɂ����āC
�E�̓W�J�}�ɂ����āC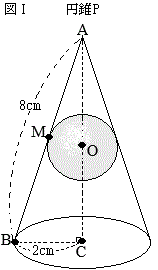 �m11�n
�m11�n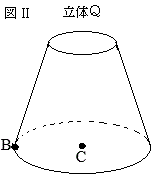 ��R�@�E���}�U�̂悤�ɁC�}�T�̉~��
��R�@�E���}�U�̂悤�ɁC�}�T�̉~��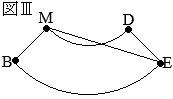 (2)�@�}�V�͗���
(2)�@�}�V�͗���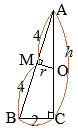 ��Q�@�E�}�ɂ�����
��Q�@�E�}�ɂ�����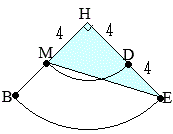 (2)�@�E�}�ɂ����āC
(2)�@�E�}�ɂ����āC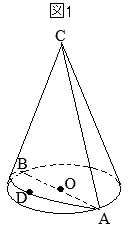 �m12�n
�m12�n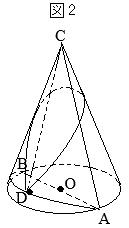 �i�E�j�@���̉~�����̑��ʏ�ɁC�}�Q�̂悤�ɓ_
�i�E�j�@���̉~�����̑��ʏ�ɁC�}�Q�̂悤�ɓ_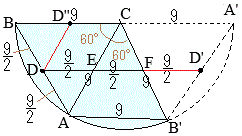 �C�Ōv�Z�����悤�ɁC��`
�C�Ōv�Z�����悤�ɁC��`