|
■平方根の復習
2乗したときに
だから,
2次方程式
【例】
(1)
(2) (3)
○肩の2を取る代わりに相手に±√が付く
○自分(x)が楽になれば,相手(a)は苦しくなる 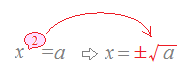 |
【問題1】 次の2次方程式の解を求めてください. (下の選択肢から選んでください)  誤答の場合: 誤答の場合:   [第1問 / 全8問]次の問題 解説↓
x2=3 →
|
|
■平方根の復習
2乗したときに
だから,
2次方程式
【例】
(1)
(2) (3)
○肩の2を取る代わりに相手に±√が付く
○自分(x)が楽になれば,相手(a)は苦しくなる 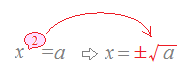 |
【問題1】 次の2次方程式の解を求めてください. (下の選択肢から選んでください)  誤答の場合: 誤答の場合:   [第1問 / 全8問]次の問題 解説↓
x2=3 →
|
|
すなわち のような2次方程式も解くことができます. ※この変形方法を使えば,別の頁で扱っている「因数分解による解き方」では解けないような問題でも解くことができます.この変形方法を使えば,どんな2次方程式でも解くことができますが,その結果は「2次方程式の解の公式」にまとめられているので,ここで無理に覚える必要はありません. ここでは,単に
x+k=Xとおくと
【例】元に戻すと のように解けます.
(1)
3を移項すると → ※7は平行根 ※3は移項によって符号が逆になることに注意 (2) −2を移項すると → 2+3=5 , 2−3=−1だからx=−1, 5 ※(1) ※(2)のように分ければ簡単になるものは,x=2±3の形ではなく,x=−1, 5のように分けなければならない. |
【問題2】 次の2次方程式の解を求めてください. (下の選択肢から選んでください)   [第1問 / 全8問]次の問題 解説↓
(x+3)2=2 →
|