|
=== �ǎ҂��z�F��ύX�������ꍇ ===
���O���̐F��ς���ɂ́C���̐F���N���b�N
|
��Փx�̖ڈ� ���ȏ����x���̊�{�F������
�Q�l���̕��ʃ��x���F���Q��
��w������{���x���F������
|
|
=== �ǎ҂��z�F��ύX�������ꍇ ===
���O���̐F��ς���ɂ́C���̐F���N���b�N
|
��Փx�̖ڈ� ���ȏ����x���̊�{�F������
�Q�l���̕��ʃ��x���F���Q��
��w������{���x���F������
|
|
�y�T. ��ԃx�N�g���̓��ρz
(1) �}�`�I�Ɏ������ꍇ �@�Q�̃x�N�g�� (2) �����\������Ă���ꍇ |
�y���1�z������
(1)�@���̂Q�̃x�N�g���̓��� (1) (2) (3) (2) (3) |
|
�y���2�z������
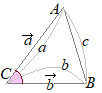
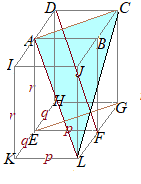
�@�E�}�̂悤�ɂP�ӂ̒�����a (>0)�̗�����ABCD-EFGH������Ƃ��C���̓��ς����߂Ă��������D  (1)
(1) (2) (3) (4) (5)
• �Q�́u�x�N�g���̑傫���v�Ɓu�x�N�g���̂Ȃ��p�v��������C���ς����܂�D
(1) ������ (2) ������
• �p�x�������ĂȂ��Ă��C�R�ӂ̒������狁�܂邱�Ƃ�����D
(3) �����`�̑Ίp���̒����͎O�����̒藝�ŋ��܂����ɁC
�i�ʉ��j������̏������͌�Ŏg���I
 �E�}�ɂ�����
�E�}�ɂ��������̖��ɖ߂�� 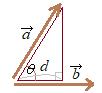 •
• �Ⴆ�C�E�}�̂悤��  (4)
(4)��AFG�́C��AFG=90���̒��p�O�p�`������ ����ɂ��  (5)
(5)�E�}�̂悤�ɁC�^����ꂽ�����ׂ̗̂ɓ����傫���̗����̂���ׂ�� �ɂȂ�C����� ������(3)�ɂ����ĕӂ̒���������ς����߂��菇���Q�l�ɂ���� |
�y���3�z������
(1)�@�E�}�̂悤�ɕӂ̒�����EF=p, EH=q, EA=r (>0) 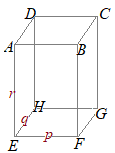 �̒�����ABCD-EFGH������Ƃ��C���̓��ς����߂Ă��������D
�̒�����ABCD-EFGH������Ƃ��C���̓��ς����߂Ă��������D(1) (2) (3) (4) (5)
�@���̖��ł́C�x�N�g���̂Ȃ��p��,���ڂɐ��l�Ƃ��ė^�����Ă��Ȃ�
�̂悤�ɁC���p�O�p�`�̕ӂ̔�ŗ]����\�����A�������͑O�q�̗��(3)�̂悤�ɁC�R�ӂ̒����œ��ς�\���Ƃ悢
�i�ʉ��j��������\�����g���l����
(2)
�i�ʉ��j
(3)����
�i�ʉ��j
(4)����
�i�ʉ��j
 (5)
(5)�E�}�̂悤�ɁC�����傫���̒����̂���O�ɕ��ׂ�� ������
�i�ʉ��j
|
|
�y�U. ��ԃx�N�g���̑傫���ƂȂ��p�z
(2) �x�N�g�� (3) �Q�̃x�N�g��
�y���1�z������
�m�����ǂށn�@�x�N�g�� �i2011�N�x��t�H�Ƒ� �H�w���j
|
�y���2�z������
�m�����ǂށn�@��Ԃ̂R�_A(1, −2, 3), B(3, −4, 2), C(−3, 3, 0)�ɑ��āC�x�N�g�� �i2005�N�x���䌧����j
|
|
�y���3�z������
�m�����ǂށn�@O�����_�Ƃ�����W��ԓ��ɂR�_ A(1, 1, 1), B(2, −1, 2), C(0, 1, 2)������D�_P���l�ʑ�OABC�̕�BC����Ƃ��C (1) ���� (2) ��AOP�̑傫�����ŏ��ɂȂ�Ƃ��̓_P�̍��W�����߂�D �i2000�N�x�L����j
(1)
(2) ��AOP=���Ƃ����� ��AOP=���̑傫�����ŏ��ɂȂ�ɂ́Ccos�����ő�ɂȂ�悢�C���̂��߂ɂ� �� ���̂Ƃ� |
�y���4�z������
�m�����ǂށn�@���W��ԓ��̓_A(4, 4, −3)��ʂ�C�_B(7, 1, 3)�����������̏���ړ����铮�_P������DP�����_O�ɍł��߂Â��Ƃ��̋���OP���ł���D �i2000�N�x���{�b��{�Y��j
|
|
�y���5�z���Q��
�m�����ǂށn�@xyz��Ԃ�3�_��A(4,5,6), B(7,11,−3), C(4,9,4)�Ƃ��C2�_A,B��ʂ钼����l�Ƃ���D (1) t��}��ϐ��Ƃ��āCl��̓_�̍��W(x, y, z)��t��p���ĕ\���D (2) �_C����̋������ŏ��ƂȂ�l��̓_H�̍��W�ƃx�N�g�� (3) �傫��1�̃x�N�g�� �i2000�N�x���u�Б� �H�w���j
(1)
y=5+6t z=6−9t (2) l��̓_P(4+3t, 5+6t, 6−9t)��C(4,9,4)�̊Ԃ̋��������߂�D ������ ���̂Ƃ��CH(5,7,3)�C 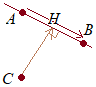 �i�ʉ��j
�i�ʉ��jCP��AB�̂Ƃ�CP���ŏ��ɂȂ� �ȉ��͓��l |
�m�����ǂށn
(3)
C(4,9,4), H(5,7,3), A(4,5,6), B(7,11,−3), �ɑ��āC���߂�x�N�g����
�@�^����ꂽ�Q�̃x�N�g���ɐ����ȒP�ʃx�N�g���������߂���̂́C�p�o�E�K�{���ŁC�����������������̂ł͂Ȃ��D
�@+�A�@�����C���̖��Ɍ����āC���z�������C���ʂ��S�`���S�`�����Ă��āC�����ɂ��ǂ蒅���Ă��C�����Ă��鎩�M�����ĂȂ��D �@�����C�̓ŁI 2x−4z=0 x=2z �@−�A 4y−2z=0 z=2y �ȏォ�� x=4y, z=2y ������B�ɑ������� |
|
�y�V. �x�N�g���̕��s�����E���������z
(1) �Q�̃x�N�g�� (2) �Q�̃x�N�g�� �i������������̎����{�ł���C���s�ɂȂ�j (2’) �R�_P, Q, R���꒼����ɂ��邽�߂̏����� ��Q, R���n�_�Ƃ��ď����Ă��悢 |
�y���6�z������
�m�����ǂށn�@ �i2014�N�x��t�H�Ƒ�j
|
|
�y���7�z������
�m�����ǂށn�@ �i2014�N�x�k���H�Ƒ�j
���߂�x�N�g����
x�������������� (1)�~2−(2) (5)��(1)�ɑ�� (5)(6)��(3)�ɑ�� (4)�ɂ��x>0������ |
�y���8�z������
�m�����ǂށn�@��Ԃ�3�_A(2, 2, 2), B(1, 2, 1), C(2, y, 1)���^�����Ă���D�O�p�`ABC�����p�O�p�`�ɂȂ�̂�y=�n�̂Ƃ��ł���D �i2011�N�x������ ���w���j
�ł��邩�� �A�j AB��BC�̂Ƃ� �@����͐��藧���Ȃ� �C�j BC��CA�̂Ƃ� �@ �E�j CA��AB�̂Ƃ� �@����͐��藧���Ȃ� �ȏォ��C�C�j���y=2����i���j |
|
�y���9�z������
�m�����ǂށn�@�_A, B, C�̍��W���CA(x, 4, −1), B(3, 1, 0), C(1, y, 1)�ł���Ƃ��CA, B, C���꒼���ɂȂ�悤��x, y�̒l���߂�D �i2000�N�x����o�ϑ�j
A, B, C���꒼���ɂȂ�ɂ́C
A, C���n�_�Ƃ��ď����Ă��悢���CB���n�_�Ƃ��ď����ƁCx, y�̌W�������̐��ɂȂ�C�v�Z�~�X��h����
�����ɕ������ y−1=3t���(2) 1=−t���(3) (3)���� t=−1 (1)�ɑ�� −2=−(x−3) x−3=2 x=5����i���j (2)�ɑ�� y=−2����i���j |
�y���10�z������
�m�����ǂށn�@�Q�̃x�N�g�� �i2016�N�x���� ���H�w���j
���߂�x�N�g����
(1)+(2) (4)��(1)�ɑ�� (4)(5)��(3)�ɑ�� ���� |
|
==�O�p�`�̖ʐ�==
�y�W. �x�N�g���ŕ\���ꂽ�O�p�`�̖ʐρz
(1)�@��ABC�ɂ����� ������ ������C(2)��(1)�ɑ������� 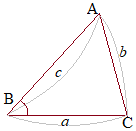 (2)�@�x�N�g���̐��������炩�łȂ��C�x�N�g���̑傫���i�ӂ̒����j�������������Ă���Ƃ��́C�u�]���藝�v��p���Ċp�x�����߂邱�Ƃ��ł���D
(2)�@�x�N�g���̐��������炩�łȂ��C�x�N�g���̑傫���i�ӂ̒����j�������������Ă���Ƃ��́C�u�]���藝�v��p���Ċp�x�����߂邱�Ƃ��ł���D�@�Ⴆ�C�E�}�ɂ����� |
�y���11�z������
�m�����ǂށn�@4�_O(0, 0, 0), A(a, 0, 0), B(0, b, 0), C(0, 0, c)�_�Ƃ���l�ʑ̂��l����D�������Ca, b, c>0�Ƃ���D�ȉ��̖�ɓ�����D (1) ��ABC�̖ʐς����߂�D (2)(3) �� �i2005�N�x����c�� ���H�w���j
|
|
==�l�ʑ̂̑̐�==
�y���12�z������
�m�����ǂށn�@�ӂ̒����� (1)�@��AOB�̗]��cos��AOB�����߁C ��AOB�̖ʐς��v�Z����D (2)�@���� (3)�@�_C������AOB���܂ޕ��ʂɐ���ℓ�������C���̕��ʂ�ℓ�Ƃ̌�_��H�Ƃ���D���̂Ƃ��C (4)�@����CH�̒��������߁C�l�ʑ�OABC�̑̐ς��v�Z����D �i2005�N�x�d�C�ʐM��j
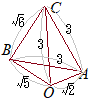 (1) ��AOB�ɂ��āCOA=a, OB=b, AB=d, ��AOB=���Ƃ����ƁC�]���藝�ɂ��
(1) ��AOB�ɂ��āCOA=a, OB=b, AB=d, ��AOB=���Ƃ����ƁC�]���藝�ɂ����AOB�̖ʐς�S�Ƃ���� 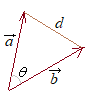 (2)
(2)�E�}�̏ꍇ ������ ���l�ɂ��� (3) (A)��� (B)��� (A’)(B’)���s=t=1 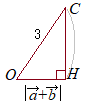 (4)
(4)������
�̐�(V)=��ʐ�(��OAB)�~����(CH)��3
|
�y���13�z���Q��
�m�����ǂށn�@�l�ʑ�ABCD�ɂ����āCAB=4, BC=5, AC=AD =BD=CD=3�Ƃ���D�_D����O�p�`ABC���܂ޕ��ʂ���DH�����낷�D���̂Ƃ��C���̖₢�ɓ�����D (1) (2) (3)�@�l�ʑ�ABCD�̑̐�V�����߂�D �i2021�N�x�É��� ���w���j
 (1)
(1)���l�ɂ���
��Ŏg���̂ŁC���łɋ��߂Ă�����
(2)�����ŁC (1)�ŋ��߂��l�C���̉�����g���� (1)�ŋ��߂��l�C���̉�����g���� �@�A��� (3)
�̐�(V)=��ʐ�(��ABC)�~����(HD)��3�@�ɂ���Čv�Z����
(1)�ŋ��߂��l����CAB��AC��������ABC�͒��p�O�p�`�܂�(1)�ŋ��߂��l�C(2)�̌��ʁC���̉��肩��
AH���狁�߂Ă��悢
|
|
�y�X.��Ԃ̂S�_�����ꕽ�ʏ�ɂ��邽�߂̏����z
�@�قȂ�R�_A, B, C�����꒼����ɂȂ��Ƃ��C�S�_A, B, C, D�����ꕽ�ʏ�ɂ��邽�߂̏����� �����藧���Ƃł���D�is, t�͎����j 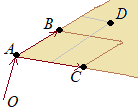 �@�R�_A, B, C�����꒼����ɂȂ��Ƃ��C
�@�R�_A, B, C�����꒼����ɂȂ��Ƃ��C�@�Ȃ��C���Ƃ���x�N�g���C�\�����x�N�g���̑g�ݍ��킹���́C���ʂ���\ |
�y���14�z������
�m�����ǂށn�@4�_A(3,1,1), B(2,−1,0), C(0,1,2), D(x,0,−1)�����ꕽ�ʏ�ɂ���悤�ɒ萔x�̒l���߂�D �ɂ��āC ���̘A����������������
�i�ʉ��j
�R�_A(3,1,1), B(2,−1,0), C(0,1,2)��ʂ镽�ʂ̕����������߂ām=���̕��@�͋��ȏ��I��{�n�C���̕��ʏ��D(x,0,−1)������Ƃ������Ƃ���萔x�̒l�����߂���@
�R�_A,B,C��ʂ镽�ʂ̕�������ax+by+cz+d=0�Ƃ���
���̕��ʂ��C�_D(x,0,−1)��ʂ邩��• �_A(3,1,1)��ʂ邩�� 3a+b+c+d=0���(1) • �_B(2,−1,0)��ʂ邩�� 2a−b+d=0���(2) • �_C(0,1,2)��ʂ邩�� b+2c+d=0���(3) ���m���S�C������3�̘A���������ɂȂ邩��C�ꕶ��d�ɂ��Ă͉������ɁCd���p�����[�^�Ƃ��đ��̖��m����d�ŕ\�����Ƃɂ���D�i�E�ӂ̊��ʂň͂����ɂ��Ă͉����Ȃ��j 2a−b=(−d)���(2’) b+2c=(−d)���(3’) ������ ���ʂ̕������� −x+3+4=0 x=7 |
|
�y���15�z���Q��
�m�����ǂށn�@���W��Ԃ̌��_��O�Ƃ��C���W��ԓ���4�_A(1, 3, 3), B(1, 1, 2), C(2, 3, 2), P(t, t, t)���Ƃ�D������t�͎����ł���D (1)�@t��0�Ƃ���Ƃ��C (2)�@ (3)�@4�_A, B, C, P���P�̕��ʂɊ܂܂��悤��t�̒l�����߂Ȃ����D �i2014�N�x�c��`�m�� �Ō��Êw���j
(1)
(2) �́Ct=2�̂Ƃ��ŏ��l���Ƃ饥��i���j (3) ���Ȃ킿 �ƂȂ�悤�ɓ_P�̍��W���߂�Ƃ悢�D t=3−2l����A t=3−k−l����B �@�A�B��������
�i�ʉ��j
A, B, C��ʂ镽�ʂ̕�������ax+by+cz+d=0�Ƃ��� ���̕��ʂ�A(1, 3, 3)��ʂ邩�� a+3b+3c+d=0����@ ���̕��ʂ�B(1, 1, 2)��ʂ邩�� a+b+2c+d=0����A ���̕��ʂ�C(2, 3, 2)��ʂ邩�� 2a+3b+2c+d=0����B �@�A�B�͖��m��4�C������3�̘A��������������C1�����������܂�Ȃ��s����ɂȂ�D�����ŁCd�ɂ��Ă͉����Ȃ����Ƃɂ��āC���̕�����d���g���ĕ\���D a+b+2c=(−d)����A’ 2a+3b+2c=(−d)����B’ �@’−�A’ 2b+c=0 c=−2b����C �C���A’�ɑ�� a+b−4b=(−d) a=3b−d����D �C�D���B�ɑ�� 2(3b−d)+3b+2(−2b)+d=0 5b=d ���ʂ̕������� −2x+y−2z+5=0 2x−y+2z−5=0 �_P(t, t, t)�����̕��ʏ�ɂ��邽�߂ɂ� 2t−t+2t−5=0 3t=5 |
�y���16�z���Q��
�m�����ǂށn�@���W��Ԃɂ����āC�R�_A(1, 0, 0), B(0, 4, 0), C(0, 0, −2)���܂ޕ��ʂ����Ƃ���D�_P(−1, −1, −1)���畽�����ɉ��낵�������ƕ������Ƃ̌�_H�̍��W���N�ł���D�܂��C�_P�̕������Ɋւ��đΏ̂ȓ_Q�̍��W���P�ł���D �i2016�N�x���� �H�w���j
 H�͂R�_A, B, C���܂ޕ��ʏ�ɂ��邩��Cs, t�������Ƃ��āC���̌`�ɏ�����D
H�͂R�_A, B, C���܂ޕ��ʏ�ɂ��邩��Cs, t�������Ƃ��āC���̌`�ɏ�����D(1)(2)�������� ���̂Ƃ� ������ ���������� |
|
�y���17�z���Q��
�m�����ǂށn�@��ԓ��ɂS�_A(1, 0, 0), B(0, −1, 0), C(0, 0, −1), D(1, 1, 1)������D (1) �R�_A, B, C��ʂ镽�ʂ����Ƃ���D�_P(x, y, z)������ɂ���Ƃ��Cx, y, z�̊Ԃɐ��藧�W�������߂�D (2) �_D���畽�����ɉ��낵�������̑���H�Ƃ���D�_H�̍��W�����߂�D �i2005�N�x���Ɍ����� ���w���j
(1)
−s=(y) −t=(z) s, t����������ƁCx−y−z=1����i���j
�i�ʉ��j
(2)�R�_A, B, C��ʂ镽�ʂ̕�������ax+by+cz+d=0�Ƃ����� �_A(1, 0, 0)��ʂ邩�� a+d=0 �_B(0, −1, 0)��ʂ邩�� −b+d=0 �_C(0, 0, −1)��ʂ邩�� −c+d=0 d(��0)��p����a, b,c��\���� a=−d, b=d, c=d ���ʂ̕������� −dx+dy+dz+d=0 x−y−z−1=0����i���j H(p, q, r)�Ƃ����ƁC H(p, q, r)�͕�������ɂ��邩�� p−q−r−1=0����B �@�A�B��������
�i�ʉ��j
�_D(1, 1, 1)��ʂ�C�������̖@���x�N�g�� �̌`�ɏ������Ƃ��ł���D���Ȃ킿 �_H(p, q, r)���������̕�����x−y−z−1=0�������� (1+t)−(1−t)−(1−t)−1=0 1+t−1+t−1+t−1=0 3t=2 |
�y���18�z������
�m�����ǂށn�@���W��ԓ���3�_A(1, 1, 2), B(3, 5, 7), C(4, 4, 5)������D�܂��Cs, t�͎����ł���Ƃ��āC�_P(s, t, 4)���l����D (1) �_P��3�_A, B, C��ʂ镽�ʏ�ɂ��邽�߂�s, t�̊W�������߂�D (2) �_P������AB��ɂ���Ƃ���s, t�̒l�����߂�D (3) �_P��3�_A, B, C��ʂ镽�ʏ���Ƃ��C���̋O�Ղɂ��O�p�`ABC�͓�̕����ɕ�������D���̓�̕����̖ʐς̔�̒lr�����߂�D�������Cr��1�Ƃ���D �i2014�N�x���{���� �H�w���j
(1)
�_P�͂R�_A, B, C���܂ޕ��ʏ�ɂ��邩��Ck, l�������Ƃ��āC���̌`�ɏ�����D (s, t, 4)=(1, 1, 2)+k(2, 4, 5)+l(3, 3, 3) t=1+4k+3l����A 4=2+5k+3l����B �@�A�B����k, l����������s, t�̊W������� �A−�@ t−s=2k����C �B−�A 4−t=1+k����D �C−�D�~2 3t−s−8=−2 3t−s=6����i���j (2) (s, t, 4)=(1, 1, 2)+k(2, 4, 5) t=1+4k����A 4=2+5k����B �B��� �@�A�ɂ��ꂼ��������� (3) 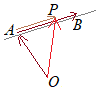 • �Q�_A, B��ʂ钼����ɓ_P������
• �Q�_A, B��ʂ钼����ɓ_P�������@�@�ik�͎����j ���̌`���悭�o�Ă��� �@�@�is+t=1, s, t�͎����j 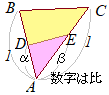 • AB:AD=1:��, AC:AE=1:���̂Ƃ�
• AB:AD=1:��, AC:AE=1:���̂Ƃ���ABC:��ADE=1:���� t=1+4k+3l����A 4=2+5k+3l����B �@�A�B����3t−s=6�̂Ƃ��Cs, t����������k, l�̊W�������� 3(1+4k+3l)−(1+2k+3l)=6 3+12k+9l−1−2k−3l=6 10k+6l=4 5k+3l=2���(*) �ƂȂ邩�� �Ƃ����� ���Ȃ킿 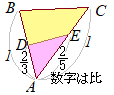 �ƂȂ邩��CAD:DB=2:1, AE:EC=2:3�ƂȂ�_���e�XD, E�Ƃ����
�ƂȂ邩��CAD:DB=2:1, AE:EC=2:3�ƂȂ�_���e�XD, E�Ƃ�����ƂȂ��āCP�͒���DE��ɂ���. �@���������� �@�@��AED : ⏢DECB=4:11
�i�ʉ��j
(2)�̌��ʂ���C �܂��C(*)����k=0�̂Ƃ��C �@���������� �@�@��AED : ⏢DECB=4:11 |