集合の要素の個数（入試問題）

=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには，次の色をクリック

◎内側の色を変えるには，次の色をクリック

◎標準文字色を変えるには，次の色をクリック

== 集合の要素の個数（入試問題） ==
難易度の目安

基　本：★☆☆

普　通：★★☆

やや難：★★★

■有限集合の要素の個数■

【問題1】★☆☆
　全体集合Uとその２つの部分集合A, Bについて，要素の個数の情報が
n(U)=80, n(A)=43, n(B)=28, n(A∩B)=16
で与えられているとき，n(A∩B)の値を求めなさい．ただし，AはAの補集合を，BはBの補集合を表す．

（2011年度日本大医学部）

［解説を読む］

公式n(A∪B)=n(A)+n(B)
−n(A∩B)
に代入すると
n(A∪B)=43+28−16
=55
n(A∩B)
=n(U)−n(A∪B)=80−55=25･･･（答） →解説を隠す←

【問題2】★☆☆
　集合A, Bが全体集合Uの部分集合で，n(A)で集合Aの要素の個数を表す．
　n(U)=100, n(A)=55, n(B)=33, n(A∩B)=22のとき，n(A∪B)=コ，n(A∪B)=サである．ここで，Bは集合Bの補集合を表す．

（2011年度北九州市立大国際環境工学部）

［解説を読む］

　公式n(A∪B)=n(A)+n(B)−n(A∩B)に代入するとn(A∪B)=55+33−22=66→コ

　n(A∪B)=n(U)−n(A∩B)（右図参照）だから
n(A∪B)=100−11=89→サ
→解説を隠す←

【問題3】★☆☆
　1から200までの自然数の集合Uを全体集合とし，Uの要素で5で割りきれるものの集合をA，7で割りきれるものの集合をBとする．このとき，A∩Bの要素の個数はウ個であり，A∩Bの要素の個数はエ個である．

（2005年度名城大理工学部）

［解説を読む］

集合Aの要素を5lとおくと
1≦5l≦200
$\frac{1}{5}\underset{=}{\lt}l\underset{=}{\lt}\frac{200}{5}$
lは整数だから
1≦l≦40
集合Bの要素を7mとおくと
1≦7m≦200
$\frac{1}{7}\underset{=}{\lt}m\underset{=}{\lt}\frac{200}{7}$
mは整数だから
1≦m≦28
集合A∩Bの要素を35nとおくと
1≦35n≦200
$\frac{1}{35}\underset{=}{\lt}n\underset{=}{\lt}\frac{200}{35}$
nは整数だから
1≦n≦5
したがって，ウ←5･･･（答）

n(A∪B)=n(A)+n(B)−n(A∩B)=40+28-5=63
n(A∩B)=n(U)−n(A∪B)=200-63=137
したがって，エ←137･･･（答）
→解説を隠す←

【問題4】★☆☆
　100から500までの整数のうち，3で割ると1余る整数全体の集合をAとし，4で割ると1余る整数全体の集合をBとする．
(1) A, B, A∩B, A∪Bの要素の個数をそれぞれ求めよ．
(2) A∪Bに含まれる整数をすべて加えた和Sを求めよ．

（2005年度宮城教育大）

［解説を読む］

(1)
　集合Aの要素を3l+1とおくと
100≦3l+1≦500
99≦3l≦499
$\frac{99}{3}\underset{=}{\lt}l\underset{=}{\lt}\frac{499}{3}$
lは整数だから
33≦l≦166
したがって，n(A)=166−33+1=134･･･（答）

（※両端を数えるときの植木算．以下も同様）

　集合Bの要素を4m+1とおくと
100≦4m+1≦500
99≦4m≦499
$\frac{99}{4}\underset{=}{\lt}m\underset{=}{\lt}\frac{499}{4}$
mは整数だから
25≦m≦124
したがって，n(B)=124−25+1=100･･･（答）
　集合A∩Bの要素を12n+1とおくと
100≦12n+1≦500
99≦12n≦499
$\frac{99}{12}\underset{=}{\lt}n\underset{=}{\lt}\frac{499}{12}$
nは整数だから
9≦n≦41
したがって，n(A∩B)=41−9+1=33･･･（答）
　A∪B=n(A)+n(B)−n(A∩B)
　=134+100−33=201･･･（答）
(2)
　集合Aに属する整数は「初項100，公差3，項数134の等差数列」だから，その和は
$S_A=\frac{134(200+ 133\times 3)}{2}=40133$
　集合Bに属する整数は「初項101，公差4，項数100の等差数列」だから，その和は
$S_B=\frac{100(202+ 99\times 4)}{2}=29900$
　集合A∩Bに属する整数は「初項109，公差12，項数33の等差数列」だから，その和は
$S_{A\cap B}=\frac{33(218+ 32\times 12)}{2}=9933$
S=40133+29900−9933=60100･･･（答）
→解説を隠す←

【問題5】★☆☆
　有限集合Xの要素の個数をn(X)で表す．n(A)=8, n(B)=9, n(C)=10, n(A∩B)=2, n(B∩C)=3, n(C∩A)=4, n(A∩B∩C)=1のとき
n(A∪B∪C)=(i)である．

（2005年度北見工業大）

［解説を読む］

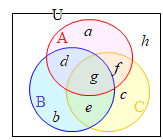３つの集合の要素の個数については，次の公式が成り立つ
n(A∪B∪C)
=n(A)+n(B)+n(C)
−n(A∩B)
−n(B∩C)
−n(C∩A)
+n(A∩B∩C)
この公式に値を代入すると
n(A∪B∪C)=8+9+10−2−3−4+1=19･･･（答） →解説を隠す←

【問題6】★☆☆
　集団検診でA, B, Cの3種類の検査を100人を対象におこなった．受診者のうち，A検査に86人，B検査に92人，C検査に78人が合格した．これらのうち，BとC二つの検査に73人，CとA二つの検査に70人，AとB二つの検査に84人が合格し，3種いずれの検査にも合格しなかったのは3人であった．3種の検査のすべてに合格したのはア人である．

（2009年度立命館大薬学部）

［解説を読む］

n(A∪B∪C)=100−3=97
また
n(A∪B∪C)=n(A)+n(B)+n(C)
−n(A∩B)−n(B∩C)−n(C∩A)+n(A∩B∩C)
だから
97=86+92+78−73−70−84+n(A∩B∩C)
n(A∩B∩C)=68→ア
→解説を隠す←

【問題7】★☆☆
　U={x|1≦x≦121, xは自然数}
を全体集合とし，Uの部分集合A, B, Cを以下により定める．

A={x|1≦x≦121, xは2で割ると1余る自然数}
B={x|1≦x≦121, xは3で割ると1余る自然数}
C={x|1≦x≦121, xは5で割ると1余る自然数}

　A, B, Cの補集合をそれぞれA, B, Cで表す．ただし，有限集合Xの要素の個数をn(X)で表す．
(1)　AアUである．

また，3イA，n(A)ウn(U)である．
ただし，ア～ウについては，以下の○0　～⑤からそれぞれ１つを選べ．ここで，同じものを何回選んでもよい．
　　○0　= 　①< 　②> 　③∈ 　④⊂ 　⑤⊃

(2)　Aの要素は，kを，0≦k≦エオを満たす整数として，カk+キと表すことができる．したがって，n(A)=クケであり，n(A)=コサである．
(3)　集合B∩Cの要素は，lを，0≦l≦シを満たす整数として，スセl+ソと表すことができる．
　したがって，n(B∩C)=タである．
　また，n(B∪C)=チツ，n(B∪C)=テトナである．
(4)　n(A∩B∩C)=ニである．

（2014年度法政大理工学部）

［解説を読む］

(1)
A⊂U→④
3∈A→③
n(A)<n(U)→①
(2)
Aの要素

0≦x=2k+1≦121→カキ
−1≦2k≦120
kは整数だから
0≦k≦60→エオ
n(A)=61→クケ
n(A)=121−61=61→コサ

(3)
B∩Cの要素

0≦x=15l+1≦121→スセ, ソ
−1≦15l≦120
lは整数だから
0≦l≦8→シ
n(B∩C)=9→タ

n(B∪C)=n(B)+n(C)−n(B∩C)について

n(B)：0≦3m+1≦121→0≦m≦40→m(B)=41
n(C)：0≦5n+1≦121→0≦n≦24→m(B)=25
n(B∪C)=41+25−9=57→チツ

n(B∪C)について

B∪C=B∩C
n(B∪C)=n(B∩C)=n(U)−n(B∩C) =121−9=112→テトナ

(4)
n(A∩B∩C)について

1≦30x+1≦121とおく（xは整数）
0≦30x≦120
xは整数だから
0≦x≦4
n(A∩B∩C)=5→ニ

→解説を隠す←

【問題8】★★☆
　集合UをU={n|nは $5\lt\sqrt{n}\lt 6$ を満たす自然数}で定め，また，Uの部分集合P, Q, R, Sを次のように定める．

P={n|n∈Uかつnは4の倍数}
Q={n|n∈Uかつnは5の倍数}
R={n|n∈Uかつnは6の倍数}
S={n|n∈Uかつnは7の倍数}

　全体集合をUとする．集合Pの補集合をPで表し，同様にQ, R, Sの補集合をそれぞれQ, R, Sで表す．
(1) Uの要素の個数はタチ個である．
(2) 次の○0　～④で与えられた集合のうち，空集合であるものはツ，テである．

　ツ，テに当てはまるものを，次の○0　～④のうちから一つずつ選べ．ただし，ツ，テの解答の順序は問わない．
　⓪P∩R　①P∩S　②Q∩R
　　③P∩Q　④R∩Q
(3) 集合Xが集合Yの部分集合であるとき，X⊂Yと表す．このとき，次の○0　～④のうち，部分集合の関係について成り立つものはト，ナである．
　ト，ナに当てはまるものを，次の○0　～④のうちから一つずつ選べ．ただし，ト，ナの解答の順序は問わない．
　⓪P∪R⊂Q　①S∩Q⊂P　②Q∩S⊂P
　　③P∪Q⊂S　④R∩S⊂Q

（2014年度センター試験数学Ⅰ･A）

［解説を読む］

(1)
$5\lt\sqrt{n}\lt 6\Longrightarrow 25\lt n\lt 36$ だからn=26,27,28,...,34,35の10個→タチ
(2)

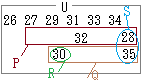右図から，空集合となるのは
⓪④→ツ，テ
(3)
各々の集合の要素を列挙すると
P∪R={28, 30, 32}
Q={26, 27, 28, 29, 31,32, 33, 34}
　　30∉QだからP∪R⊂Qは成り立たない
S∩Q={28}
P={28,32}
　　だからS∩Q⊂Pは成り立つ
Q∩S={26,27,28,29,31,33,34,35}
P={26,27,29,30,31,33,34,35}
　　28∉PだからQ∩S⊂Pは成り立たない
P∪Q={26,27,28,29,30,31,32,33,34,35}
S={26,27,29,30,31,32,33,34}
　　28,35∉Sだから P∪Q⊂Sは成り立たない
R∩S={26,27,29,31,32,33,34}
Q={26,27,28,29,31,32,33,34}
　　だからR∩S⊂Qは成り立つ
①④→ト，ナ →解説を隠す←

【問題9】★★☆
　全体集合Xを30以下の自然数の集合とし，Xの部分集合A, Bをそれぞれ
A={x|xは3の倍数}，B={x|xは5の倍数}
とする．また，Xの部分集合Sに対して，Sの補集合をSと書くこととする．
(1)　A∪BとA∩Bを，それぞれ要素を書き並べる方法で表せ．
(2)　A∩Bの要素の個数を求めよ．
(3)　CをXの部分集合で，以下の4つの条件を満たすものとする．

①Cの要素の個数は8
②A∩Cの要素の個数は5
③B∩Cの要素の個数は4
④A∩B∩Cの要素の個数は2

　このとき，C∩(A∪B)の要素の個数を求めよ．

（2000年度東京理科大工学部）

［解説を読む］

(1)

	B	B
A	15,30	3,6,9,12,18 21,24,27
A	5,10,15,20,25	1,2,4,7,8, 11,13,14,16,17, 19,22,23,26,28, 29

要素を書き並べると，右の表のようになる．
A∪B
={3,5,6,9,10,12,
15,18,20,21,24,
25,27,30}
A∩B={15,30}
(2)
n(A∩B)16 (3)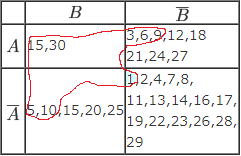

②Aから5個
③Bから4個
④A∩Bから2個
①全部で8個
となるように組合せるには，例えば右図の赤線内をCとすればよい
このとき，C∩(A∪B) には水色の背景色で示した１個だけが入る →解説を隠す←

【問題10】★★☆
　全体集合Xを25以下の自然数の集合とし，Xの部分集合AとBをそれぞれ
A={x|xは3の倍数}，B={x|xは4の倍数}
とする．次の問いに答えよ．
(1)　A∪BとA∩Bを，それぞれ要素を書き並べる方法で示せ．
(2)　A∪Bの要素の個数を求めよ．
(3)　CはXの部分集合で，以下の3つの条件を満たすものとする．このとき， C∩(A∪B)の要素の個数を求めよ．

条件①A∩Cの要素の個数は4
条件②B∩Cの要素の個数は3
条件③A∩B∩Cの要素の個数は1

（2011年度徳島文理大理工学部）

［解説を読む］

(1)

	B	B
A	12,24	3,6,9,15,18 21
A	4,8,16,20	1,2,5,7,10, 11,13,14,17, 19,22,23,25

要素を書き並べると，右の表のようになる．
A∪B
={3,4,6,8,9,12,15,16,
18,20,21,24}
A∩B={12,24}
(2)
n(A∪B)=23
(3)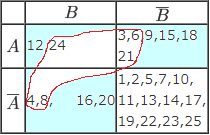

②Aから4個
③Bから3個
④A∩Bから1個
となるように組合せるには，例えば右図の赤線内をCとすればよい
　このとき，C∩(A∩B)には何個の要素が入るかは定まらない（０個の場合から13個の場合まであり得る．図では０個の場合の例を示している．）しかし，C∩(A∩B)の要素の個数は，(3)の結果に影響しない．
C∩(A∪B)=6（水色の背景色で示したもの） →解説を隠す←

...（PC版）メニューに戻る