== 漸化式と一般項 ==
■ 数列の漸化式(帰納的定義)から一般項を求める問題をするとき,一体どこまでやればよいのか迷うところがあります.
-
漸化式を数学Aの1,2年の授業でするとすれば,5時間もすれば多い方でしょう.また,3年生で数学Aが追加で設定されていて,時間的に余裕がある場合でも漸化式に10時間も割り当てられることはめったにないと思います.
-
漸化式の解法を型ごとに覚えていくという取り扱いでは,暗記色の強いものとなります.
-
時間不足のままで,特性方程式を利用した解法に触れると,階差数列や文字係数の問題にまで特性方程式を持ち出す答案が現れ,答案がもつれてしまうことがあります.
-
他方では,大学入試問題で,漸化式の解法が直接問われることは,教科書レベルの問題を小問として問う場合を除けば,意外に少なく,(私立大学や公立大学で時々見かける程度です)誘導問題として解法が指定されているものが多く見られます.
-
このような現状で,「漸化式はやればやるだけ点が取れる」とはいえず,労力と時間を多量に投入するのは疑問です.
ここでは,「生徒の実力:少しはできるが特別できるわけではない」「使える時間:5時間程度」と想定して,効果/時間比のよい方法を考えてみます.(結論から言えば,「定型的問題を,等比数列にする方法です.」)
(非定型的問題は,推定+数学的帰納法でしょう.)
■ 問題と解答の例
《問題》 次の答案を読んで,類題に答えなさい.(それぞれの問題をクリックすれば答案が出ます.)
1
a1=1, an+1=2an+1 (n=1,2,3,・・・) |
類題1-1,2,3 |
2
a1=1, an+1=an+2 (n=1,2,3,・・・) |
類題2-1,2,3 |
| |
|
3
a1=3, an+1=3an+2n−1 (n=1,2,3,・・・) |
類題3-1,2,3 |
4
a1=3, an+1=3an+2n (n=1,2,3,・・・) |
類題4-1,2,3 |
5
a1=1, an+1=nan (n=1,2,3,・・・) |
類題5-1,2,3 |
| |
|
6
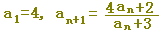 |
未 |
7
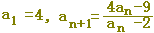 |
未 |
| |
|
8
a1=1,a2=2, an+2−3an+1+2an=0 (n=1,2,3,・・・) |
類題8-1,2,3 |
9
a1=2,b1=1, an+1=2an+2bn, bn+1=an+3bn (n=1,2,3,・・・) |
類題9-1,2,3 |
|