次の不等式の表わす領域を下の図のうちから選びなさい.
(図をクリックすれば採点結果と解説が出ます)
[第1問 / 全16問]

(1)まず, \( y=2x+ 1 \)の直線を考えます \( y=2x+ 1 \)の直線を考えます
→y切片が1で,傾きが2の直線
(2)次に,その直線の「上側」の領域を答にします
(1)まず, \( y=x-2 \)の直線を考えます \( y=x-2 \)の直線を考えます
→y切片が−2で,傾きが1の直線
(2)次に,その直線の「上側」の領域を答にします
(1)まず, \( y=-x+3 \)の直線を考えます \( y=-x+3 \)の直線を考えます
→y切片が3で,傾きが−1の直線
(2)次に,その直線の「上側」の領域を答にします
(1)まず, \( y=2 \)の直線を考えます \( y=2 \)の直線を考えます
→y切片が2で,傾きが0の直線(x軸に平行な直線)
(2)次に,その直線の「上側」の領域を答にします
(1)まず, \( y=2x+1 \)の直線を考えます \( y=2x+1 \)の直線を考えます
→y切片が1で,傾きが2の直線
(2)次に,その直線の「下側」の領域を答にします
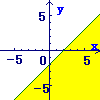
(1)まず, \( y=x-2 \)の直線を考えます \( y=x-2 \)の直線を考えます
→y切片が−2で,傾きが1の直線
(2)次に,その直線の「下側」の領域を答にします
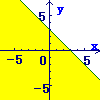
(1)まず, \( y=-x+ 3 \)の直線を考えます \( y=-x+ 3 \)の直線を考えます
→y切片が3で,傾きが−1の直線
(2)次に,その直線の「下側」の領域を答にします
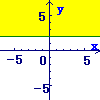
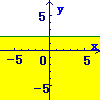
(1)まず, \( y=2 \)の直線を考えます \( y=2 \)の直線を考えます
→y切片が2で,傾きが0の直線(x軸に平行な直線)
(2)次に,その直線の「下側」の領域を答にします
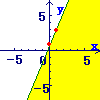
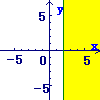
(1)まず, \( x=2 \)の直線を考えます \( x=2 \)の直線を考えます
→x切片が2で,y軸に平行な直線
(2)次に,その直線の「右側」の領域を答にします
(1)まず, \( x^2+ y^2=25 \)の円を考えます \( x^2+ y^2=25 \)の円を考えます
→原点を中心とする半径5の円
(2)次に,その円の「内側」の領域を答にします
(1)まず, \( x^2+ y^2=9 \)の円を考えます \( x^2+ y^2=9 \)の円を考えます
→原点を中心とする半径3の円
(2)次に,その円の「内側」の領域を答にします
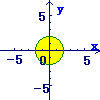
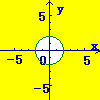
(1)まず, \( x^2+ y^2=4 \)の円を考えます \( x^2+ y^2=4 \)の円を考えます
→原点を中心とする半径2の円
(2)次に,その円の「内側」の領域を答にします
(1)まず, \( x=2 \)の直線を考えます \( x=2 \)の直線を考えます
→x切片が2で,y軸に平行な直線
(2)次に,その直線の「左側」の領域を答にします
(1)まず, \( x^2+ y^2=25 \)の円を考えます \( x^2+ y^2=25 \)の円を考えます
→原点を中心とする半径5の円
(2)次に,その円の「外側」の領域を答にします
(1)まず, \( x^2+ y^2=9 \)の円を考えます \( x^2+ y^2=9 \)の円を考えます
→原点を中心とする半径3の円
(2)次に,その円の「外側」の領域を答にします
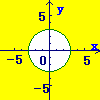
(1)まず, \( x^2+ y^2=4 \)の円を考えます \( x^2+ y^2=4 \)の円を考えます
→原点を中心とする半径2の円
(2)次に,その円の「外側」の領域を答にします
→閉じる←

下図の黄色の部分.ただし境界線は含まないものとする.







|