センター試験.数Ⅱ･B-指数.対数関数(2013～)

...(ＰＣ版)メニューに戻る
*** 科目 ***
数Ⅰ・Ａ数Ⅱ・Ｂ数Ⅲ 高卒・大学初年度
*** 単元 ***
式と証明点と直線円軌跡と領域三角関数
指数関数対数関数微分不定積分定積分
高次方程式数列漸化式と数学的帰納法
平面ベクトル空間ベクトル確率分布

※高校数学Ⅱの「対数関数」について，このサイトには次の教材があります．
この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください．　が現在地です．

↓対数の定義

↓対数計算
↓同(2)
↓対数関数のグラフ
↓底の変換公式
↓同(2)
↓対数計算（各停）

↓対数方程式（解説）
↓同（問題）
↓対数不等式

↓常用対数

↓指数が対数のもの

↓指数･対数（入試問題）
↓センター試験指数･対数 2006年～
センター試験指数･対数 2013年～

=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには，次の色をクリック

◎内側の色を変えるには，次の色をクリック

◎標準文字色を変えるには，次の色をクリック

== センター試験.数Ⅱ･B-指数.対数関数(2013～) ==

【2013年度センター試験.数学Ⅱ･B】第1問[2]（必答問題）

　連立方程式

(＊)

x + y + z = 3

2^{x} + 2^{y} + 2^{z} = \frac{35}{2}

\frac{1}{2^{x}} + \frac{1}{2^{y}} + \frac{1}{2^{z}} = \frac{49}{16}

を満たす実数x, y, zを求めよう。ただし，x≦y≦zとする。

X = 2^{x}, Y = 2^{y}, Z = 2^{z}

とおくと，x≦y≦zによりX≦Y≦Zである。(＊)から，X, Y, Zの関係式

X Y Z =

ソ

X + Y + Z = \frac{35}{2}

X Y + Y Z + Z X =

タチ

ツ

が得られる。

解説を読む

【指数と対数の関係】

p = \log_{a} M ⟺ a^{p} = M

ただし，a>0, a≠1, M>0

X = 2^{x}, Y = 2^{y}, Z = 2^{z}

だから

X Y Z = 2^{x} \times 2^{y} \times 2^{z}

= 2^{x + y + z} = 2^{3} = 8

→ソ

2^{x} + 2^{y} + 2^{z} = \frac{35}{2}

だから

X + Y + Z = \frac{35}{2}

\frac{1}{X} + \frac{1}{Y} + \frac{1}{Z} = \frac{49}{16}

だから

\frac{X Y + Y Z + Z X}{X Y Z} = \frac{49}{16}

X Y + Y Z + Z X = \frac{49}{16} X Y Z = \frac{49}{2}

→タチツ
→解説を隠す←

　この関係式を利用すると,tの3次式(t−X)(t−Y)(t−Z)は

(t - X) (t - Y) (t - Z)

= t^{3} - (X + Y + Z) t^{2} + (X Y + Y Z + Z X) t - X Y Z

= t^{3} - \frac{35}{2} t^{2} +

タチ

ツ

t -

ソ

= (t - \frac{1}{2}) (t -

テ

) (t -

トナ

)

となる。したがって，X≦Y≦Zにより

X = \frac{1}{2}, Y =

テ，

Z =

トナ
となり，

x = \log

ニ

X, y = \log

ニ

Y, z = \log

ニ

Z

から
x=ヌネ，y=ノ，z=ハ
であることがわかる。

解説を読む

(t - X) (t - Y) (t - Z) = t^{3} - \frac{35}{2} t^{2} + \frac{49}{2} t - 8

= (t - \frac{1}{2}) (t^{2} - 17 t + 16)

= (t - \frac{1}{2}) (t - 1) (t - 16)

→テ,トナ

X = \frac{1}{2}, Y = 1, Z = 16

により

x = \log_{2} X, y = \log_{2} Y, z = \log_{2} Z

→ニ

x = \log_{2} X = \log_{2} (\frac{1}{2}) = - 1

→ヌネ

y = \log_{2} Y = \log_{2} 1 = 0

→ノ

z = \log_{2} Z = \log_{2} 16 = 4

→ハ

♪∀～勝手に批評～個人の感想～∅♥
　教科書レベルの基本問題であり，確実に得点すべき問題です．

→解説を隠す←

【2014年度センター試験.数学Ⅱ･B】第1問[2]（必答問題）

　自然数m, nに対して，不等式

\log_{2} m^{3} + \log_{3} n^{2} ≦ 3

･･･④
を考える。

　m=2, n=1のとき，

\log_{2} m^{3} + \log_{3} n^{2} =

ソであり，このm, nの組は④を満たす。
　m=4, n=3のとき，

\log_{2} m^{3} + \log_{3} n^{2} =

タであり，このm, nの組は④を満たさない。

　不等式④を満たす自然数m, nの組の個数を調べよう。④は

\log_{2} m +

チ

ツ

\log_{3} n ≦

テ･･･⑤

と変形できる。
　nが自然数のとき，

\log_{3} n

のとり得る最小の値はトであるから，⑤により，

\log_{2} m ≦

テでなければならない。

\log_{2} m ≦

テにより，m=ナまたはm=ニでなければならない。ただし，ナ<ニとする。

解説を読む

\log_{2} 2^{3} + \log_{3} 1^{2} = 3 \log_{2} 2 + 2 \log_{3} 1 = 3 + 0 = 3

→ソ

\log_{2} 4^{3} + \log_{3} 3^{2} = 3 \log_{2} 4 + 2 \log_{3} 3 = 6 + 2 = 8

→タ

3 \log_{2} m + 2 \log_{3} n ≦ 3

\log_{2} m + \frac{2}{3} \log_{3} n ≦ 1

→チ,ツ,テ

nが自然数のとき，

\log_{3} n ≦ 0

→ト(等号はn=1のとき)

\log_{2} m ≦ 1

により
m=1またはm=2→ナ,ニ
→解説を隠す←

m=ナの場合，⑤は，

\log_{3} n ≦

ヌ

ネ

となり，

n2≦ノハと変形できる。よって，m=ナのとき，⑤を満たす自然数nのとり得る値の範囲はn≦ヒである。したがって，m=ナの場合，④を満たす自然数m, nの組の個数はヒである。
　同様にして，m=ニの場合，④を満たす自然数m, nの組の個数はフである。
　以上のことから，④を満たす自然数m, nの組の個数はヘである。

解説を読む

m=1のとき，⑤は

\log_{2} 1 + \frac{2}{3} \log_{3} n ≦ 1

\frac{2}{3} \log_{3} n ≦ 1

\log_{3} n ≦ \frac{3}{2}

→ヌ,ネ

2 \log_{3} n ≦ 3

\log_{3} n^{2} ≦ 3

n^{2} ≦ 27

→ノハ

n ≦ 5

→ヒ

m=2のとき，④は

\log_{2} 2^{3} + \log_{3} n^{2} ≦ 3

3 \log_{2} 2 + \log_{3} n^{2} ≦ 3

\log_{3} n^{2} ≦ 0

n^{2} ≦ 1

n = 1

→1(組)→フ
以上から，5組と1組で6組→ヘ →解説を隠す←

【2016年度センター試験.数学Ⅱ･B】第1問[1]（必答問題）

(1)　

8^{\frac{5}{6}} =

ア

\sqrt{}

イ　，

\log_{27} \frac{1}{9} =

ウエ

オ

である。

(2)

y = 2^{x}

のグラフと

y = (\frac{1}{2})^{x}

のグラフはカである。

y = 2^{x}

のグラフと

y = \log_{2} x

のグラフはキである。

y = \log_{2} x

のグラフと

y = \log_{\frac{1}{2}} x

のグラフはクである。

y = \log_{2} x

のグラフと

y = \log_{2} \frac{1}{x}

のグラフはケである。

　カ～ケに当てはまるものを，次の⓪～③のうちから一つずつ選べ。ただし,同じものを繰り返し選んでもよい。

⓪ 同じもの

① x軸に関して対称

② y軸に関して対称

③ 直線y=xに関して対称

解説を読む

(1)

8^{\frac{5}{6}} = (2^{3})^{\frac{5}{6}} = 2^{\frac{5}{2}} = \sqrt{32} = 4 \sqrt{2}

→ア,イ

【底の変換公式】

\log_{a} b = \frac{\log_{c} b}{\log_{c} a}

ただし，(a, b, c>0)かつ(a, c≠1)

\log_{27} \frac{1}{9} = \frac{\log_{3} \frac{1}{9}}{\log_{3} 27} = \frac{\log_{3} 3^{- 2}}{\log_{3} 3^{3}}

= \frac{- 2 \log_{3} 3}{3 \log_{3} 3} = \frac{- 2}{3}

→ウエ,オ

(2)

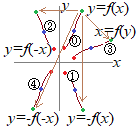《x軸に関して対称》
　　右図の⓪と①
《y軸に関して対称》
　　右図の⓪と②
《y=xの直線に関して対称》
　　右図の⓪と③
《原点に関して対称》
　　右図の⓪と④

f (x) = 2^{x}, g (x) = (\frac{1}{2})^{x}

とおくと

g (x) = 2^{- x} = f (- x)

だから
　　これらはy軸に関して対称:②→カ

y = 2^{x}

は

x = \log_{2} y

に等しい．これに「y=xの直線に関して対称」なグラフは，

y = \log_{2} x

　　y=xの直線に関して対称:③→キ

\log_{2} x, g (x) = \log_{\frac{1}{2}} x

とおくと

g (x) = \frac{\log_{2} x}{\log_{2} \frac{1}{2}} = \frac{\log_{2} x}{- 1} = - \log_{2} x = - f (x)

だから，これらはx軸に関して対称:①→ク

f (x) = \log_{2} x, g (x) = \log_{2} \frac{1}{x}

とおくと

g (x) = \log_{2} x^{- 1} = - \log_{2} x = - f (x)

だから
　　これらはx軸に関して対称:①→ケ
→解説を隠す←

(3) x>0の範囲における関数

y = (\log_{2} \frac{x}{4})^{2} - 4 \log_{4} x + 3

の最小値を求めよう。

t = \log_{2} x

とおく。このとき，y=t2−コt+サである。また，xがx>0の範囲を動くとき，tのとり得る値の範囲はシである。シに当てはまるものを，次の⓪～③のうちから一つ選べ。

⓪ t>0

① t>1

② t>0かつt≠1

③ 実数全体

　したがって，yはt=スのとき，すなわちx=セのとき，最小値ソタをとる。

解説を読む

y = (\log_{2} \frac{x}{4})^{2} - 4 \log_{4} x + 3

= (\log_{2} x - \log_{2} 4)^{2} - 4 \frac{\log_{2} x}{\log_{2} 4} + 3

= (\log_{2} x - 2)^{2} - 4 \frac{\log_{2} x}{2} + 3

= (\log_{2} x - 2)^{2} - 2 \log_{2} x + 3

t = \log_{2} x (x > 0)

とおくと

y = (t - 2)^{2} - 2 t + 3 = t^{2} - 6 t + 7

(tは全実数)→コ,サ
tのとり得る値の範囲は，③実数全体→シ

y = (t - 3)^{2} - 2

と変形できるから
t=3すなわちx=8のとき，最小値−2をとる→ス,セ,ソ,タ
→解説を隠す←

【2017年度センター試験.数学Ⅱ･B】第1問[2]（必答問題）

　座標平面上に点

A (0, \frac{3}{2})

をとり，関数

y = \log_{2} x

のグラフ上に2点

B (p, \log_{2} p), C (q, \log_{2} q)

をとる。線分ABを1:2に内分する点がCであるとき， p, qの値を求めよう。

　真数の条件により，p>タ，q>タである。ただし，対数

\log_{a} b

に対し，aを底といい，bを真数という。

　線分ABを1:2に内分する点の座標は，pを用いて

(

チ

ツ

テ

ト

\log_{2} p +

ナ

)

と表される。これがCの座標と一致するので

チ

ツ

p=q 　･･････④

テ

ト

\log_{2} p +

ナ

= \log_{2} q

　･･････⑤

が成り立つ。

解説を読む

真数条件よりp>0→タ

A (0, \frac{3}{2}), B (p, \log_{2} p)

を1:2に内分する点の座標は

= (\frac{2 \times 0 + 1 \times p}{1 + 2}, \frac{2 \times \frac{3}{2} + 1 \times \log_{2} p}{1 + 2})

= (\frac{1}{3} p, \frac{1}{3} \log_{2} p + 1)

→チ,ツ,テ,ト,ナ
→解説を隠す←

　⑤は

ニ

ヌ

qネ　･･････⑥

と変形できる。④と⑥を連立させた方程式を解いて，
p>タ，q>タに注意すると
p=ノ

\sqrt{}

ハ　，q=ヒ

\sqrt{}

フ　
である。

　また，Cのy座標

\log_{2} (

ヒ

\sqrt{}

フ　

)

の値を，小数第2位を四捨五入して小数第1位まで求めると，ヘである。ヘに当てはまるものを，次の⓪～ⓑのうちから一つ選べ。ただし，

\log_{10} 2 = 0.3010, \log_{10} 3 = 0.4771,

\log_{10} 7 = 0.8451

とする。

　⓪ 0.3　① 0.6　② 0.9　③ 1.3　④ 0.6　⑤ 1.9
　⑥ 2.3　⑦ 2.6　⑧ 2.9　⑨ 3.3　ⓐ 3.6　ⓑ 3.9

解説を読む

⑤は

\log_{2} p + 3 = 3 \log_{2} q

\log_{2} p + l o g_{2} 8 = \log_{2} q^{3}

\log_{2} 8 p = \log_{2} q^{3}

8 p = q^{3}

p = \frac{q^{3}}{8}

→ニ,ヌ,ネ
と変形できる．④⑥の連立方程式を解くと

p = 6 \sqrt{6}, q = 2 \sqrt{6}

→ノ,ハ,ヒ,フ

\log_{2} (2 \sqrt{6}) = \log_{2} 2 + \log_{2} \sqrt{6}

= 1 + \frac{1}{2} \log_{2} 6

= 1 + \frac{1}{2} (\log_{2} 2 + \log_{2} 3)

= \frac{3}{2} + \frac{1}{2} \times \frac{\log_{10} 3}{\log_{10} 2}

= 1.5 + 0.5 \times \frac{0.4771}{0.3010}

=1.5+0.5×1.585
≒1.5+0.792≒1.5+0.8=2.3→⑥ ヘ

♪∀～勝手に批評～個人の感想～∅♥
　教科書レベルの基本問題であり，確実に得点すべき問題です．なお，この問題では

\log_{10} 7

の値は書いてなくても解ける．

→解説を隠す←

【2018年度センター試験.数学Ⅱ･B】第1問[2]（必答問題）

　cを正の定数として，不等式

x^{\log_{3} x} ≦ (\frac{x}{c})^{3}

　･･･②
を考える。

　3を底とする②の両辺の対数をとり，

t = \log_{3} x

とおくと
tソ−タt+タ

\log_{3} c ≧ 0

　･･･③
となる。ただし，対数

\log_{a} b

に対し，aを底といい，bを真数という。

\sqrt[3]{9}

のとき，②を満たすxの値の範囲を求めよう。③により
t≦チ，t≧ツ
である。さらに，真数の条件も考えて
テ<x≦ト，x≧ナ
となる。

解説を読む

【真数が指数関数になっている式は簡単になる】

【指数が対数関数になっている式は簡単になる】

x^{\log_{3} x} ≧ (\frac{x}{c})^{3}

の両辺に3を底とする対数をとると

\log_{3} (x^{\log_{3} x}) ≧ \log_{3} (\frac{x}{c})^{3}

(\log_{3} x) (\log_{3} x) ≧ 3 \log_{3} (\frac{x}{c})

(\log_{3} x) (\log_{3} x) ≧ 3 (\log_{3} x - \log_{3} c)

t = \log_{3} x

とおくと

t^{2} ≧ 3 (t - \log_{3} c)

t^{2} - 3 t + 3 \log_{3} c ≧ 0

→ソ,タ

c = \sqrt[3]{9}

のとき

3 \log_{3} c = 3 \log_{3} \sqrt[3]{9} = 3 \log_{3} 9^{\frac{1}{3}} = 3 \times \frac{1}{3} \log_{3} 9

= \log_{3} 3^{2} = 2 \log_{3} 3 = 2

だから，不等式は

t^{2} - 3 t + 2 ≧ 0

(t - 1) (t - 2) ≧ 0

t≦1, t≧2→チ,ツ
さらに

\log_{3} x ≦ 1, \log_{3} x ≧ 2

より，真数条件も考えると
0<x≦3, x≧9→テ,ト,ナ
→解説を隠す←

　次に，②がx>テの範囲でつねに成り立つようなcの値の範囲を求めよう。
　xがx>テの範囲を動くとき，tのとり得る値の範囲はニである。ニに当てはまるものを，次の⓪～③のうちから一つ選べ。

⓪　正の実数全体

①　負の実数全体

②　実数全体

③　1以外の実数全体

　この範囲のtに対して，③がつねに成り立つための必要十分条件は，

\log_{3} c ≧

ヌ

ネ

である。すなわち，c≧ノ

\sqrt{}

ハヒ　

である。

解説を読む

xがx>0の範囲を動くとき

t = \log_{3} x

のとり得る値の範囲は，実数全体②→ニ
この範囲のtに対して

t^{2} - 3 t + 3 \log_{3} c ≧ 0

がつねに成り立つための必要十分条件は

D = (- 3)^{2} - 12 \cdot \log_{3} c ≦ 0

\log_{3} c ≧ \frac{9}{12} = \frac{3}{4}

→ヌ,ネ
すなわち

c ≧ 3^{\frac{3}{4}} = \sqrt[4]{27}

→ノ,ハヒ

♪∀～勝手に批評～個人の感想～∅♥
　教科書レベルの基本問題であり，確実に得点すべき問題です．

→解説を隠す←

【2019年度センター試験.数学Ⅱ･B】第1問[2]（必答問題）

　連立方程式

\log_{2} (x + 2) - 2 \log_{4} (y + 3) = - 1

　･･･②

(\frac{1}{3})^{y} - 11 (\frac{1}{3})^{x + 1} + 6 = 0

　･･･③
を満たす実数x, yを求めよう。

　真数の条件により，x, yのとり得る値の範囲はタである。タに当てはまるものを，次の⓪～⑤のうちから一つ選べ。ただし，対数

\log_{a} b

に対し，aを底といい，bを真数という。

⓪ x>0, y>0

① x>2, y>3

② x>−2, y>−3

③ x<0, y<0

④ x<2, y<3

⑤ x<−2, y<−3

　底の変換公式により

\log_{4} (y + 3) =

\log_{2} (y + 3)

チ

である。よって，②から
y=ツx+テ　･･･④
が得られる。

解説を読む

真数条件から
x+2>0, y+3>0
x>−2, y>−3→②タ
底の変換公式から

\log_{4} (y + 3) = \frac{\log_{2} (y + 3)}{\log_{2} 4} = \frac{\log_{2} (y + 3)}{2}

→チ
よって②から

\log_{2} (x + 2) - 2 \times \frac{\log_{2} (y + 3)}{2} = - 1

\log_{2} (x + 2) - \log_{2} (y + 3) = - 1

\log_{2} (x + 2) + 1 = \log_{2} (y + 3)

2 (x + 2) = y + 3

y = 2 x + 1

→ツ,テ ④
→解説を隠す←

　次に，

t = (\frac{1}{3})^{x}

とおき，④を用いて③をtの方程式に書き直すと
t2−トナt+ニヌ=0　･･･⑤
が得られる。また，xがタにおけるxの範囲を動くとき，tのとり得る値の範囲は
ネ<t<ノ　･･･⑥
である。
　⑥の範囲で方程式⑤を解くと，t=ハとなる。したがって，連立方程式②，③を満たす実数x, yの値は

x = \log_{3}

ヒ

フ

，

y = \log_{3}

ヘ

ホ

であることがわかる。

解説を読む

④の

y = 2 x + 1

を③に代入すると

(\frac{1}{3})^{2 x + 1} - 11 (\frac{1}{3})^{x + 1} + 6 = 0

{(\frac{1}{3})^{x}}^{2} \times \frac{1}{3} - 11 (\frac{1}{3})^{x} \times \frac{1}{3} + 6 = 0

t = (\frac{1}{3})^{x}

とおくと

t^{2} \times \frac{1}{3} - 11 t \times \frac{1}{3} + 6 = 0

t^{2} - 11 t + 18 = 0

→トナ,ニヌ
x>−2のとき，0<t<9→ネ,ノ
⑤の解t=2, 9のうち，⑥の範囲にあるのは，t=2→ハ
このとき

x = \log_{\frac{1}{3}} 2 = \frac{\log_{3} 2}{\log_{3} \frac{1}{3}} = - \log_{3} 2 = \log_{3} (\frac{1}{2})

→ヒ,フ

y = 2 x + 1 = 2 \log_{3} (\frac{1}{2}) + 1 = \log_{3} \frac{1}{4} + \log_{3} 3

= \log_{3} \frac{3}{4}

→ヘ,ホ →解説を隠す←

【2020年度センター試験.数学Ⅱ･B】第1問[2]（必答問題）

(2)　x, yは正の実数とする。連立不等式

\log_{3} (x \sqrt{y}) ≦ 5

　･･･②

\log_{81} \frac{y}{x^{3}} ≦ 1

　･･･③
について考える。
　

X = \log_{3} x, Y = \log_{3} y

とおくと，②は
ヌX+Y≦ネノ　･･･④
と変形でき，③は
ハX−Y≧ヒフ　･･･⑤
と変形できる。
　X, Yが④と⑤を満たすとき，Yのとり得る最大の整数の値はヘである。また，x, yが②，③と

\log_{3} y =

ヘを同時に満たすとき，xのとり得る最大の整数の値はホである。

解説を読む

【連立不等式の解き方】
●「連立方程式」は，２つの式を足したり，引いたりして１つの文字だけにして解く．これに対して

2X+Y≦10
3X−Y≧−4
のような「連立不等式」は，"２つの式を足したり，引いたりする変形"を行わない方がよい･･･変形すると"必要条件に変わってしまい"，元の範囲よりも広い範囲になる．
●「連立不等式」⇒「１つずつ図示」して，共通部分を調べるとよい．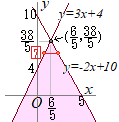

②より

\log_{3} x + \log_{3} \sqrt{y} ≦ 5

\log_{3} x + \frac{1}{2} \log_{3} y ≦ 5

2 \log_{3} x + \log_{3} y ≦ 10

X = \log_{3} x, Y = \log_{3} y

とおくと

2 X + Y ≦ 10

→ヌ,ネノ

③より

\log_{81} y - \log_{81} x^{3} ≦ 1

\frac{\lg_{3} y}{\log_{3} 81} - \frac{\log_{3} x^{3}}{\log_{3} 81} ≦ 1

ここで，

\log_{3} 81 = \log_{3} 3^{4} = 4 \log_{3} 3 = 4

だから

\frac{\lg_{3} y}{4} - \frac{\log_{3} x^{3}}{4} ≦ 1

\log_{3} y - \log_{3} x^{3} ≦ 4

\lg_{3} y - 3 \log_{3} x ≦ 4

X = \log_{3} x, Y = \log_{3} y

とおくと

Y - 3 X ≦ 4

3 X - Y ≧ - 4

→ハ,ヒフ

2X+Y=10と3X−Y=−4の交点の座標は

(\frac{6}{5}, \frac{38}{5})

したがって，Y≦7→ヘ
Y=7と3X−Y=−4の交点のX座標は

X = 1

Y=7と2X+Y=10の交点のX座標は

X = \frac{3}{2}

したがって，Y=7のとき

1 ≦ X ≦ \frac{3}{2}

1 ≦ \log_{3} x ≦ \frac{3}{2}

3^{1} ≦ x ≦ 3^{\frac{3}{2}}

3 ≦ x ≦ \sqrt{27}

整数ではx≦5→ホ
→解説を隠す←

...（携帯版）メニューに戻る

...（PC版）メニューに戻る

髫ｨ�ｽ�ｿ�ｽ驍ｵ�ｺ髦ｮ蜻ｻ�ｿ�ｽ驛｢�ｧ�ｽ�ｵ驛｢�ｧ�ｽ�､驛｢譏懶ｽｺ�･�ｽ�ｽ驍ｵ�ｺ�ｽ�ｮGoogle髫ｶﾂ隲幢ｿｽ�ｽ�ｴ�ｽ�｢髫ｨ�ｽ�ｿ�ｽ

髫ｨ�ｽ�ｽ�ｳ驍ｵ�ｺ髦ｮ蜻ｻ�ｿ�ｽ驛｢譎擾ｽ｣�ｹ�ｽ�ｽ驛｢�ｧ�ｽ�ｸ驍ｵ�ｺ�ｽ�ｮ髯ｷ閧ｲ�｣�ｯ�ｽ�ｽ�ｽ�ｭ驍ｵ�ｺ�ｽ�ｫ髫ｰ魃会ｽｽ�ｻ驛｢�ｧ鬩ｫﾂ霎滂ｽ｡驍ｵ�ｲ�ｽ�ｽ驛｢�ｧ�ｽ�｢驛｢譎｢�ｽ�ｳ驛｢�ｧ�ｽ�ｱ驛｢譎｢�ｽ�ｼ驛｢譎会ｽ｣�ｯ�つ遶擾ｽｽ�ｽ�ｿ�ｽ�｡驍ｵ�ｲ�ｽ�ｽ
… 驍ｵ�ｺ髦ｮ蜻ｻ�ｿ�ｽ驛｢�ｧ�ｽ�｢驛｢譎｢�ｽ�ｳ驛｢�ｧ�ｽ�ｱ驛｢譎｢�ｽ�ｼ驛｢譎冗樟�ｽ�ｽ髫ｰ�ｨ陷ｻ蜿夜ｧ�垈�ｾ�ｽ�ｹ髯懈ｻゑｽｿ�ｽ�ｽ�ｽ髯ｷ�ｿ郢ｧ迺ｰﾂ�ｽ�ｽ遶企豪�ｸ�ｺ髴域喚髮ｷ驍ｵ�ｺ�ｽ�ｦ驍ｵ�ｺ�ｽ�ｽ隨ｳ�ｽ�ｸ�ｺ�ｽ�ｽ驍ｵ�ｺ鬮ｦ�ｪ遶擾ｽｪ驍ｵ�ｺ�ｽ�ｽ

髫ｨ�ｽ�ｿ�ｽ驍ｵ�ｺ髦ｮ蜻ｻ�ｿ�ｽ鬯ｯ�ｽ�ｽ遶企豪�ｸ�ｺ�ｽ�､驍ｵ�ｺ�ｽ�ｽ遯ｶ�ｻ�ｽ�ｽ霑ｹ螢ｽ�ｽ驍ｵ�ｺ�ｽ�ｽ陜ｨ謚ｵ�ｿ�ｽ隴ｴ�ｧ邵ｺ讙趣ｽｸ�ｺ�ｽ�ｽ陜ｨ謚ｵ�ｿ�ｽ驕停或�ｿ�｣鬯ｩ謌奇ｽｼ雋ｻ�ｼ讓抵ｽｸ�ｺ�ｽ�ｮ髫ｰ蜴�ｽｿ�ｽ鬩包ｽｭ�ｽ�ｽ陟募ｨｯ關ｽ驍ｵ�ｺ�ｽ�ｮ髣皮判縺假ｿｽ�ｽ髫ｲ�｢雋企ｳｶ�ｦ驍ｵ�ｺ陟募ｨｯ譌ｺ驛｢�ｧ陟暮ｯ会ｽｿ�ｽ鬯ｨ�ｾ遶擾ｽｽ�ｽ�ｿ�ｽ�｡驍ｵ�ｺ陷会ｽｱ遯ｶ�ｻ驍ｵ�ｺ闕ｳ蟯ｩ蜻ｳ驍ｵ�ｺ髴郁ｲｻ�ｼ讖ｸ�ｿ�ｽ�ｽ�ｽ

髫ｨ�ｳ陋ｹ�ｺ隴ｫ螟撰ｿｽ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｮ髯溷私�ｽ�｢驛｢�ｧ陋幢ｽｵ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｦ驍ｵ�ｺ�ｽ�ｽ�ｽ邇厄ｽｫ�｢雋企ｳｶ�ｦ驍ｵ�ｺ�ｽ�ｯ髯ｷ闌ｨ�ｽ�ｨ鬯ｩ蟷｢�ｽ�ｨ鬮ｫ�ｱ�ｽ�ｭ驍ｵ�ｺ�ｽ�ｾ驍ｵ�ｺ陝ｶ蜷ｮﾂ�ｻ驛｢�ｧ郢ｧ�ｽ�ｽ閾･�ｸ�ｺ�ｽ�｣驍ｵ�ｺ�ｽ�ｦ驍ｵ�ｺ�ｽ�ｽ遶擾ｽｪ驍ｵ�ｺ陷ｻ�ｻ�ｽ�ｼ�ｽ�ｽ
髫ｨ�ｳ陋ｹ�ｺ隨渉髫ｲ�ｽ�ｽ�ｳ驍ｵ�ｺ�ｽ�ｮ髯ｷﾂ�ｽ�ｽ邵ｲ謚ｵ�ｿ�ｽ陟募ｨｯ�ｽ驍ｵ�ｺ�ｽ�ｮ髯懶ｿｽ陜楢ｶ｣�ｽ�｡陟募ｨｯﾂ�ｲ驍ｵ�ｺ�ｽ�ｩ驍ｵ�ｺ�ｽ�ｽ邵ｲ蝣､�ｸ�ｺ郢ｧ�ｽ螟｢驍ｵ�ｺ雋�ｼ会ｽｰ驛｢�ｧ陷ｻ闌ｨ�ｽ�ｭ�ｽ�｣鬩墓慣�ｽ�ｺ驍ｵ�ｺ�ｽ�ｪ髫ｴ�ｽ�ｿ�ｽ�ｽ�ｫ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｧ髣費ｽｨ隴擾ｽｴ遶擾ｽｴ驍ｵ�ｺ�ｽ�ｦ驍ｵ�ｺ�ｽ�ｽ隨ｳ�ｽ�ｸ�ｺ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｽ隨ｳ�ｽ�ｬ�ｾ�ｽ�ｹ髯懈ｻゑｽｿ�ｽ�ｽ�ｦ遶擾ｽｵ隰泌調�ｸ�ｺ�ｽ�ｫ髯晢ｿｽ�ｽ�ｾ驍ｵ�ｺ陷会ｽｱ遯ｶ�ｻ驍ｵ�ｺ�ｽ�ｯ�ｽ�ｽ隰疲ｺｷ�ｺ�ｽ螯呻ｿｽ�ｽ驍ｵ�ｺ�ｽ�ｪ鬯ｮ�ｯ髣企ｯ会ｽｽ鬘俶ｱ橸ｿｽ�ｾ髯滂ｽ｢隲帛ｲｩ�ｽ驛｢�ｧ闕ｵ譎｢�ｽ閧ｲ�ｸ�ｺ�ｽ�ｽ遶企豪�ｸ�ｺ陷会ｽｱ遯ｶ�ｻ驍ｵ�ｺ�ｽ�ｽ遶擾ｽｪ驍ｵ�ｺ陷ｻ�ｻ�ｽ�ｼ髮懶ｽ｣�ｽ�ｼ鬩包ｽｺ�つ�ｽ�ｻ驍ｵ�ｺ�ｽ�ｪ驍ｵ�ｺ陞ゑｿｽ�ｽ�ｼ隴ｴ�ｧ陋ｻ�､髫ｰ�ｦ�ｽ�ｽ陜趣ｽｪ驍ｵ�ｺ�ｽ�ｪ髫ｴ�ｽ�ｿ�ｽ�ｽ�ｫ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｫ驍ｵ�ｺ�ｽ�ｪ驍ｵ�ｺ�ｽ�｣驍ｵ�ｺ�ｽ�ｦ驍ｵ�ｺ�ｽ�ｽ�ｽ邇匁捗�ｽ�ｴ髯ｷ�ｷ陋ｹ�ｻ�ｽ�ｽ�ｽ�ｽ陟募ｨｯ關ｽ驛｢�ｧ陟暮ｯ会ｽｽ螳壽ｦ�ｽ�ｬ鬯ｮ�｢闕ｵ譏ｶ�ｽ驛｢�ｧ闕ｵ譏ｶ�ｽ鬩包ｽｲ�ｽ�ｽ�つ�ｽ�ｽ隨�ｽ｡驍ｵ�ｺ闔会ｽ｣邵ｲ蝣､�ｸ�ｺ�ｽ�ｪ驍ｵ�ｺ陷托ｽｰ�ｽ�ｪ�ｽ�ｭ鬮｢�ｽ�ｽ�ｽ�ｽ繧句擅�ｽ�ｭ驛｢�ｧ�つ驍ｵ�ｺ髦ｮ蜷ｮ�ｽ驍ｵ�ｺ�ｽ�ｫ驍ｵ�ｺ�ｽ�ｪ驛｢�ｧ驗呻ｽｫ遶擾ｽｪ驍ｵ�ｺ陷ｷ�ｶ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｧ�ｽ�ｽ隴ｴ�ｧ雎撰ｽｻ鬨ｾ蛹�ｽｽ�ｨ驍ｵ�ｺ陷会ｽｱ遶擾ｽｪ驍ｵ�ｺ陝ｶ蜻ｻ�ｽ髮｣�ｿ�ｽ髮懶ｽ｣�ｽ�ｼ�ｽ�ｽ

鬮ｮ莨夲ｽｽ�ｪ髯懶ｿｽ闕ｳ蟯ｩ�ｽ髯晢ｿｽ�ｽ�ｾ驍ｵ�ｺ陷ｷ�ｶ�ｽ邇匁綜隶捺慣�ｽ�ｭ隴∵腸�ｿ�ｽ髣包ｽｳ�ｽ�ｭ髯晢ｿｽ�ｽ�ｦ髴大｣ｼ迴ｾ�ｽ�ｽ驍ｵ�ｺ髦ｮ蜻ｻ�ｿ�ｽ鬯ｯ�ｽ�ｿ�ｽ�ｽ�ｽ驕抵ｿｽ�ｽ�ｫ闖ｫ�ｶ�ｽ�ｽ�ｽ�｡髴大｣ｼ迴ｾ�ｽ�ｽ驍ｵ�ｺ髦ｮ蜻ｻ�ｿ�ｽ鬯ｯ�ｽ�ｿ�ｽ驍ｵ�ｺ�ｽ�ｫ驍ｵ�ｺ郢ｧ�ｽ�ｽ鬘費ｽｸ�ｺ�ｽ�ｾ驍ｵ�ｺ�ｽ�ｽ