|
【平面上の内分点,外分点の座標】
2点 (1) m : nに内分する点Pの座標は 特に,中点(1:1に内分する点)Mの座標は (2) m : n (m≠n)に外分する点Qの座標は 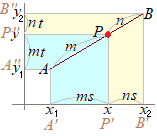 (解説)
(解説)
以下の解説は,多くの教科書に書かれているものとほぼ同じです.
(1)←
以下においては,
中学2年生で習う平行線の性質,または中学校3年生で習う相似図形の性質を使うと,右図においてAP : BP=m : nのとき,A'P' : B'P'=m : n したがって y座標についても同様に示すことができる. 中点の公式はm=n=1とすると得られる. 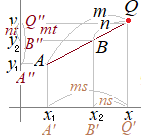 (2)←
(2)←
以下においては,
中学2年生で習う平行線の性質,または中学校3年生で習う相似図形の性質を使うと,右図においてAQ : BQ=m : nのとき,A'Q' : B'Q'=m : n したがって y座標についても同様に示すことができる. ⇒このように,内分公式のnのところに−nを代入すると,外分公式になる |
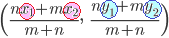

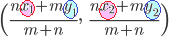 #自家受粉になっている#
#自家受粉になっている#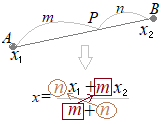 図の見かけ上は,Aの座標
図の見かけ上は,Aの座標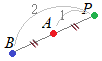 [未知数を
[未知数を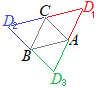 ※もし,3点A,B,Cの座標が与えられていて,「平行四辺形の第4の頂点を求めよ」という問題であれば,右図のように,回り方の順序が3通り考えられるので,(1)ACの中点がBDの中点と一致する場合,(2)BCの中点がADの中点と一致する場合,(1)ABの中点がCDの中点と一致する場合の3通りの答えを書かなければならない.
※もし,3点A,B,Cの座標が与えられていて,「平行四辺形の第4の頂点を求めよ」という問題であれば,右図のように,回り方の順序が3通り考えられるので,(1)ACの中点がBDの中点と一致する場合,(2)BCの中点がADの中点と一致する場合,(1)ABの中点がCDの中点と一致する場合の3通りの答えを書かなければならない.