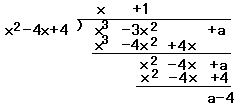
割り切れるのだから,a−4=0
a=4・・・(答)
《←メニューに戻る》《ヒントを求む→》 |
(考え方2):恒等式として係数比較を行う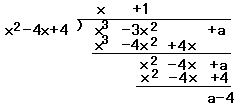
割り切れるのだから,a−4=0
a=4・・・(答)
x3−3x2+a=(x−2)2(x+b)とおく(考え方3):因数定理を習っているとき−−因数定理の繰り返し適用
(右辺)=(x2−4x+4)(x+b)=x3+(b−4)x2+(4−4b)x+4b
両辺の係数を比較すると
−3=b−4,0=4−4b,a=4b
a=4,(b=1)・・・(答)
f(x)=x3−3x2+aとおく(考え方4):微分を習っているとき−−「(x−a)2で割り切れる←→f(a)=f’(a)=0」を使う.
因数定理によりf(2)=0だから,8−12+a=0
a=4 ・・・(必要)・・・まだ(x−2)2で割り切れることを使ってないが,ここはあわてず,証明に切り替える.[穴埋め問題ならなくても可]
このとき,f(x)=x3−3x2+4=(x−2)(x2−x−2)=(x−2)2(x+1)は(x−2)2で割り切れる.(十分)
a=4・・・(答)
f(x)=x3−3x2+aとおくと,f’(x)=3x2−6x
f(2)=f’(2)=0より
8−12+a=0・・・(1)
12−12=0・・・(2):つねに成立
(1)(2)より,a=4・・・(答)