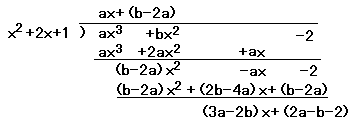
割り切れるのだから,3a−2b=0,2a−b−2=0
これより,a=4,b=6・・・(答)
《←メニューに戻る》《ヒントを求む→》 |
(考え方2):恒等式として係数比較を行う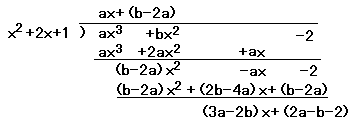
割り切れるのだから,3a−2b=0,2a−b−2=0
これより,a=4,b=6・・・(答)
ax3+bx2−2=(x2+2x+1)(ax−2)とおく(考え方3):因数定理を習っているとき−−因数定理を繰り返し適用する.
(右辺)=ax3+(2a−2)x2+(a−4)x−2 だから,係数比較により
b=2a−2,a−4=0
これより,a=4,b=6・・・(答)
f(x)=ax3+bx2−2とおく.(考え方4):微分を習っているとき−−重解条件:f(−1)=f’(−1)=0を用いる.
因数定理により,f(−1)=0 −a+b−2=0・・・(1)
(1)よりb=a+2を代入
f(x)=ax3+(a+2)x2−2=a(x3+x2)+2x2−2
=(x+1)(ax2+2x−2)
ここでg(x)=ax2+2x−2とおくと
因数定理により,g(−1)=0 a−2−2=0
ゆえに,a=4
(1)に代入してb=6・・・(答)
f(x)=ax3+bx2−2とおくと,f’(x)=3ax2+2bx
f(x)が(x+1)2で割り切れる必要十分条件は f(−1)=f’(−1)=0 だから
−a+b−2=0,3a−2b=0よりa=4,b=6・・・(答)