|
(Ⅳ) 中学校の連立方程式の文章題を生成AIで解くには?(1) 《例7》 入力欄に次のように書き込んで,Enterキーを押す 結果は次のようになる
①
ChatGTPでは,連立方程式を使って,直ちに正解に達する.家から橋まで6分,橋から学校まで Copilotでは,連立方程式を使って,直ちに正解に達する.家から橋まで6分,橋から学校まで Geminiでは,連立方程式を使って,直ちに正解に達する.家から橋まで6分,橋から学校まで
②
ChatGTPでは,合同式を使って途中経過が書かれるので,中学生には読めない.お菓子10個となって,間違い. Copilotでは,合同式を使って途中経過が書かれるので,中学生には読めない.お菓子10個となって,間違い. Geminiでは,連立方程式を使って途中経過が書かれ,お菓子30個となって,正解
③
ChatGTPでは,合同式を使って途中経過が書かれ,A組の生徒は14人となって間違い Copilotでは,合同式を使って途中経過が書かれ,A組の生徒は14人となって間違い Geminiでは,連立方程式を使って途中経過が書かれ,A組の生徒は38人となって正解
\(\Longrightarrow\)
(ここまでの感想) Gemini→連立方程式として解くと,正解に達する. ChatGPT,Copilot→合同式を使って解くときに,割る数よりも余りが多く見える場合や,余りが負の数に見える問題で間違う. |
(Ⅴ) 図形問題を文章だけで書いたものを生成AIで解くには? 《例8》 入力欄に次のように書き込んで,Enterキーを押す 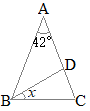 ③の図形は右図のようになっているが,この図を生成AIには渡さずに,文章だけで解くことにする.
③の図形は右図のようになっているが,この図を生成AIには渡さずに,文章だけで解くことにする.結果は次のようになる
①
ChatGTPでは,∠BAD=120°と間違え,また錯角を読み間違えて,誤答70°になる Copilotでは,二等辺三角形から∠BAD=50°と間違え,また同位角を読み間違えて,誤答70°になる Geminiでは,2つの三角形の内角の和を使って,正解55°に達する.
②
ChatGTPでは,ABCDが四角形だと考えて、誤答65°になる. Copilotでは,2つの三角形の内角の和を使って,正解115°に達する. Geminiでは,2つの三角形の内角の和を使って,正解115°に達する.
③
ChatGTPでは,AD=BDの条件の使い方を間違えて,誤答0°になる Copilotでは,∠ADBとその外角を混同して,結果は誤答15°になる. Geminiでは,2つの三角形の内角の和から計算していくが,誤答34.5°になる.
\(\Longrightarrow\)
(ここまでの感想) 三角形2個の組み合わせ図形になると,間違いが出てくる |