(Ⅸ) ベクトルの問題を解くには
《例I.4》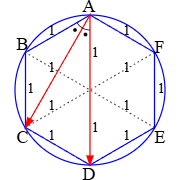 生成AIでベクトルを書き込むには,MathJaxの書き方で
生成AIでベクトルを書き込むには,MathJaxの書き方で\vec{AC}, \vec{AD} などと書くとよい. 入力欄に次のように書き込んで,Enterキーを押した場合 1. 「ChatGTP」 ⇒
途中経過が成分計算として示され,答 \(3\) になる
2. 「Copilot」 ⇒
途中経過が成分計算として示され,答 \(3\) になる
3. 「Gemini」 ⇒
途中経過が図形ベクトルを用いて示されるが,なぜか∠AOD=120°で計算してしまい,誤答になる
《例I.4》入力欄に次のように書き込んで,Enterキーを押した場合 1. 「ChatGTP」 ⇒
正解が得られ,135°となる
2. 「Copilot」 ⇒
正解が得られ,135°となる
3. 「Gemini」 ⇒
正解が得られ,\(\displaystyle\frac{3}{4}\pi\)または135°となる
⇒ここまでの実験から分かる傾向を大雑把に言えば,生成AIのベクトル計算は「成分表示では強い」が「図形表示のベクトルでは弱い」かもしれない
|
(Ⅹ) 微分の問題を解くには 商の微分法の問題 《例J.1》 入力欄に次のように書き込んで,Enterキーを押した場合 1. 「ChatGTP」 ⇒
正解が得られ,\(\displaystyle y'=\frac{7}{(2x+1)^2}\) となる
2. 「Copilot」 ⇒
正解が得られ,\(\displaystyle y'=\frac{7}{(2x+1)^2}\) となる
3. 「Gemini」 ⇒
正解が得られ,\(\displaystyle\frac{dy}{dx}=\frac{7}{(2x+1)^2}\) となる
対数微分法の問題《例J.2》 入力欄に次のように書き込んで,Enterキーを押した場合 1. 「ChatGTP」 ⇒
正解が得られ,\(\displaystyle \frac{dy}{dx}=x^{\cos x}(-\sin x\ln x+\frac{\cos x}{x}) \) となる
2. 「Copilot」 ⇒
正解が得られ,\(\displaystyle \frac{dy}{dx}=x^{\cos x}(\frac{\cos x}{x}-\ln x\cdot\sin x) \) となる
3. 「Gemini」 ⇒
正解が得られ,\(\displaystyle \frac{dy}{dx}=x^{\cos x}(-\sin x\ln x+\frac{\cos x}{x}) \) となる
陰関数の微分法《例J.3》 入力欄に次のように書き込んで,Enterキーを押した場合 1. 「ChatGTP」 ⇒
正解が得られ,\(\displaystyle \frac{dy}{dx}=\frac{4x}{9y} \) となる
2. 「Copilot」 ⇒
正解が得られ,\(\displaystyle \frac{dy}{dx}=\frac{4x}{9y}) \) となる
3. 「Gemini」 ⇒
正解が得られ,\(\displaystyle \frac{dy}{dx}=\frac{4x}{9y}) \) となる
|