数II　図形と方程式

(1) 直線 (3+2k)x-(2-k)y-12-k=0 はkの値にかかわらず定点を通る。この定点の座標は (2，3) (2，-3) (-2，3) (-2，-3) (3，2)		[数II][図形と方程式][２直線の交点を通る直線] ○a+bk=0はa=b=0のときkのどんな値についても成り立つ恒等式です。 ○(ax+by+c)+k(dx+ey+f)=0はax+by+c=0かつdx+ey+f=0となるx,yの値(２直線の交点)についてはｋのどんな値についても成り立ちます。 →(ax+by+c)+k(dx+ey+f)=0は２直線ax+by+c=0，dx+ey+f=0の交点では常に成立します。左の問題では，ア)kで整理するのが基本ですが、イ)問題文を｢信用して｣ｋに適当な値を代入する裏技もあります。ア)3x-2y-12+k(2x+y-1)=0より3x-2y-12=0と2x+y-1=0の交点(2，-3)を通るイ)k=2を代入x=2 k=0を代入3x-2y-12=0→y=-3 (※十分性の証明が必要な問題では、交点ではkの1次式の係数が２つとも0になることから上記の恒等式になるとします。)
(2) 平行な２直線3x+4y-10=0，3x+4y=0の間の距離は 1　2 3 5 10		[数II][図形と方程式][点と直線の距離] 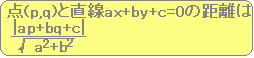左の問題では，平行な2直線の距離はどこで測っても同じなので，一方の直線3x+4y=0上の点(0，0)と3x+4y-10=0の距離を求めると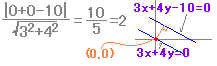
(3) ３つの直線y=-x+6，y=x+2，x+3y=6 で囲まれる三角形の面積は 2 4 6 8 10		[数II][図形と方程式][三角形の面積]
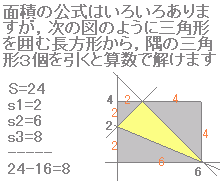(4) ２円x²+y²=9，(x-3)²+(y-2)²=2の２交点と点(3，1)を通る円の方程式は x²+y²-6x-4y=0 x²+y²-6x-2y+1=0 x²+y²-3x-2y+1=0 x²+y²=2 x²+y²=10		[数II][図形と方程式][２円の交点を通る円] ○２円x²+y²+ax+by+c=0，x²+y²+dx+ey+f=0が交わるとき， x²+y²+ax+by+c+k(x²+y²+dx+ey+f)=0 (k≠-1) は２円x²+y²+ax+by+c=0，x²+y²+dx+ey+f=0の２交点を通る円となる。(この式は円になり，かつ，２交点を通るから) 左の問題では，求める方程式を (x-3)²+(y-2)²-2+k(x²+y²-9)=0とおき，(3，1)を代入するとk=1 このとき方程式は2x²+2y²-6x-4y+2=0 すなわちx²+y²-3x-2y+1=0となります。
(5) 点Ａ(0，-5)を直線x+2y=0に関して対称移動したときの点Ｂの座標は (4，-3)　(-4，-2) (4，3)　(5，0)　(-5，0)		[数II][図形と方程式][対称移動] 左の問題では，求める点Ｂの座標を(p，q)とおくとき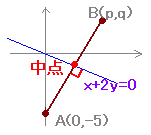ＡＢの中点が与えられた直線上にあること･･(1) ＡＢが与えられた直線に垂直になること・・(2) からp，qを求められます。
(6) ２点A(2，0)，B(-1，0)からの距離の比が2：1となる点の軌跡の方程式は x=0　 x=1 x²+y²-x-2=0 x²+y²-6x+5=0　 x²+y²+4x=0		[数II][図形と方程式][アポロニウスの円] ○２定点からの距離の比が一定な点の軌跡は円になる。(特に、内分点と外分点が直径の両端となるので，これを利用して求めてもよい。) 左の問題では，動点の座標を(x，y)とおくと AP:PB=2:1 → AP=2PB → AP²=4PB² (x-2)²+y2=4{(x+1)²+y2} 3x²+3y²+12x=0よりx²+y²+4x=0
(7) 円(x-a)²+(y-b)²=r²の周上の点(p，q)における接線の方程式は (p-a)²+(q-b)²=r² px+qy=r² p(x-a)+q(y-b)=r² (p-a)x+(q-b)y=r² (p-a)(x-a)+(q-b)(y-b)=r²		[数II][図形と方程式][円の接線の方程式] ○円x²+y²=r²の周上の点(x₀，y₀)における接線の方程式はx₀x+y₀y=r² ○点(a，b)を中心とする円では原点に移動→接線の方程式→戻す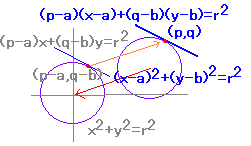左の問題では円(x-a)²+(y-b)²=r²と点(p，q)を原点が中心の円に移動すると円x²+y²=r²上の点(p-a，q-b)の接線が (p-a)x+(q-b)y=r² これをｘ方向にa，ｙ方向にｂ移動すると (p-a)(x-a)+(q-b)(y-b)=r²
(8) mが実数値をとって変化するとき，２直線y=mx，x+my-4=0の交点の軌跡は円(x-2)²+y²=4 (点(4，0)を除く) 円(x-2)²+y²=4 (点(0，0)を除く) 円x²+y²=4 (点(2，0)を除く) 円x²+y²=4 (点(-2，0)を除く) 円x²+y²=4 (点(0，2)を除く)		[数II][図形と方程式][軌跡の方程式] ○交点を求めて媒介変数を消去すると求められますが ○連立方程式←→交点だから，初めの方程式から媒介変数を消去するだけで求められます。左の問題では y=mxより，ア)x≠0のときm=y/xを代入 x+y²/x-4=0 x²+y²-4x=0 (x-2)²+y²=4 イ)x=0のときy=0はx+my-4=0を満たさないので点(0，0)は除外
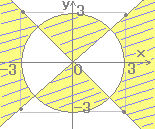
(9) 次の図の斜線部（境界線を含まない）の領域を表わす不等式は (y-x)(y+x)(x²+y²-9)>0 (y-x)(y+x)(x²+y²-9)<0 xy(x²+y²)>9 xy(x²+y²-9)>0 xy(x²+y²-9)<0		[数II][図形と方程式][軌跡の方程式] ○市松模様（チェック模様）→因数分解型不等式 (1)　境界線の方程式を・・=0の形に表わす (2)　因数分解型を作る (3)　計算しやすい点の符号に合うように<>0を選択左の問題では (1)　y-x=0，y+x=0，x²+y²-9=0 (2) (y-x)(y+x)(x²+y²-9) (3) 例えば(4，0)を該当させるには　(0-4)(0+4)(16+0-9)=(-4)(4)(7)をＯＫとする　ゆえに(y-x)(y+x)(x²+y²-9)<0
(10) 連立不等式y≦x，y≧-x+2，y≧3(x-2)で表わされる領域において(x-1)²+y²の取り得る値の最大値は 2 3 4 9 13		[数II][図形と方程式][領域内の最大・最小] ○求める値をkとおくと方程式となりグラフが描けます。左の問題では 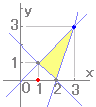(x-1)²+y²=kとおくと点(1，0)を中心とする円となり，ｋはその半径(の２乗) 頂点(3，3)が最も遠いから (3-1)²+3²=13