数II　図形と方程式

(1) ２点Ａ(-4，-3)，Ｂ(1，-2)から等距離にあるｘ軸上の点の座標は (-3，-5)　(-2，0)　(0，-10) 　(2，0)　(5，1)		[数II][図形と方程式][２点間の距離]
(2)		[数II][図形と方程式][外分点の座標]
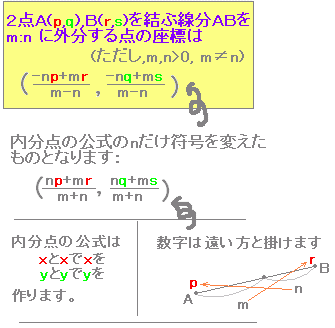(3) ２点Ａ(0，-1)，Ｂ(2，3) を結ぶ線分ＡＢの垂直二等分線の方程式は x+2y-3=0 x-2y-3=0 x-2y+1=0 x+2y-1=0 2x-y-1=0		[数II][図形と方程式][点，傾き→直線の方程式] 左の問題では ABの傾きは2、これに垂直な傾きは-1/2 ＡＢの中点は(1，1) そこで(1，1)を通り，傾き-1/2の直線の方程式を求めます。 y-1=-1/2(x-1) 2y-2=-x+1 x+2y-3=0
(4) 点(5，-1)を通り，直線2x-3y+4=0に平行な直線の方程式は 2x-3y-9=0 2x+3y-13=0 3x+2y+13=0 3x+2y-13=0 2x-3y-13=0		[数II][図形と方程式][２直線の平行条件] ○２つの直線y=mx+kとy=m'x+k'が平行　→　傾きが等しい ○ 左の問題では2x-3y+4=0→y=2/3x+4/3の傾きは2/3だから (5，-1)を通り傾き2/3の直線の方程式を求めます。 y+1=2/3(x-5)　→　2x-3y-13=0
(5) 円x²+y²-6x+8y+24=0の中心と半径は中心(-3，4)，半径1　中心(3，-4)，半径1 中心(6，-8)，半径1　中心(6，-8)，半径中心(-6，8)，半径		[数II][図形と方程式][円の方程式の一般形] ○円の方程式の標準形円(x-a)²+(y-b)²=r² (r>0)の中心は(a，b)，半径はr ○円の方程式の一般形円x²+y²+Ax+By+C=0の中心と半径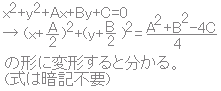左の問題では，(x-3)²+(y+4)²=1と変形すると中心(3，-4)，半径1となります。
(6) 円(x-2)²+(y+3)²=16をｘ軸の正の向きに4，ｙ軸の正の向きに-5だけ平行移動してできる円の方程式は (x-2)²+(y+3)²=4　 (x+2)²+(y-2)²=16 x²+(y+3)²=9　 (x-6)²+(y+8)²=16　 x²+y²=25		[数II][図形と方程式][円の方程式] ○円の方程式の標準形円(x-a)²+(y-b)²=r² (r>0)の中心は(a，b)，半径はr 左の問題では，円の平行移動によって半径は変わらないので，右辺は16 中心の座標は(2，-3)→(6，-8)となります。
(7) 円x²+y²=25の周上の点(3，-4)における接線の傾きは		[数II][図形と方程式][円の接線の方程式] ○円x²+y²=r²の周上の点(a，b)における接線の方程式は ax+by=r² 左の問題では，3x-4y=25となり，傾きは
(8) 直線 y=x+k が円 x²+y²=4 に接するような定数kの値は k=6 k=±6 k=±2 k=√6 k=±√6		[数II][図形と方程式][円と直線] ○円x²+y²=r²と直線y=mx+kが接する条件は，ｙを消去してｘの２次方程式について(判別式)=0で調べることができます。左の問題ではx²+(x+k)²=4 9x²+4√2kx+(k²-4)=0 D’=(k)²-9(k²-4)=0 k²=36 よりk=±6となります。
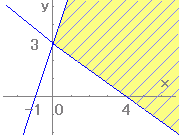
(9) 次の斜線部(境界線を含まない)で示される領域を表わす不等式は		[数II][図形と方程式][不等式と領域] ○y=mx+kの直線の上側はy>mx+kで表わされ，下側はy<mx+kで表わされます。共通部分は連立方程式で表わします。左の問題では，y=-3/4x+3の上側でy>-3/4x+3　→　4y>-3x+12 → 3x+4y-12>0 y=3x+3の下側でy<3x+3 → 3x-y+3>0 となります。
(10) 次の斜線部(境界線を含む)で示される領域において，y-3xのとる値の最大値は -2 -3 -7 -9 3		[数II][図形と方程式][領域内の最大・最小] ○領域内の最大値求める式の値を=kとおくと方程式になり、グラフが書けます。領域を通るようなグラフのうちｋが最大となるものを探します。左の問題では、y-3x=kとおくと y=3x+kの傾きは3だから右図のようにx=1，y=1でｋが最大となり、このときy-3x=1-3=-2=k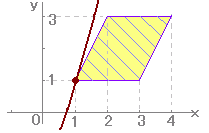