|
���O�p���̂Q�{�p����,���p�����i���K���j �@���̕łł͂Q�{�p�����C���p�������g���ȒP�Ȍv�Z���������܂��D
�y���P�z
�i�j�@������Q�ی��̊p�ŁCsin��=�̂Ƃ��C���̒l�����߂Ă��������D sin 2��, cos 2��, tan 2�� cos2��=1−sin2��=1−= cos��=− (<0) ������ sin 2��=2sin��·cos��=2××(−)=− cos 2��=cos2��−sin2��=−= tan 2��==(−)÷=− …���̖��ł�tan���̒l���܂����߂Ă��Ȃ��̂ŁC��L�̂悤�ɋ��߂邱�Ƃ��ł��܂��Dtan��=−�̒l�����߂Ă���tan 2���̂Q�{�p�������g�����@������܂��D
�y���Q�z
sin22.5���̒l�����߂Ă��������D ���p�������g���C
�i�j�@cos 2���̒l���������sin ��, cos ��, tan ���̒l�����܂�D ���̖��ł� �@cos45���̒l���������sin22.5��, cos22.5��, tan22.5���̒l�����܂�D sin222.5��=== sin22.5��= (>0) |
�y�Q�{�p�����z
�@�Q�{�p�����͉��@�藝�ɂ�������=���Ƃ����Γ����܂��D ��sin(��+��)=sin��·cos��+cos��·sin���ɂ�������=���Ƃ����ƁC sin2��=2sin��·cos�� ��cos(��+��)=cos��·cos��−sin��·sin���ɂ�������=���Ƃ����ƁC cos2��=cos2��−sin2�� =1−2 sin2�� (←cos2��=1−sin2���ɂ��ό`) =2 cos2��−1 (←sin2��=1−cos2���ɂ��ό`) ��tan(��+��)=�ɂ�������=���Ƃ����ƁC tan2��= �y���p�����z �@���p������cos2���̌������t�ɉ����Γ����܂��D�isin2��, tan2���̌�������͓����܂���D�j ��cos2��=1−2 sin2�����t�ɉ����� sin2��= ���Ȃ킿 ��cos2��=2 cos2��−1���t�ɉ����� cos2��= ���Ȃ킿 ��tan2��=�ɂ�� tan2��= ���Ȃ킿 |
|
�y���P�z
�@������R�ی��̊p�ŁCcos��=−�̂Ƃ��C���̒l�����߂Ă��������D sin 2��, cos 2��, tan 2�� �ɓ�����̂��E�̑I��������I��ł��������D
|
|
|
�@���͑�R�ی��̊p������sin��<0�ɂȂ�C sin��=−=(1) ������ |
−
−
−
|
|
sin2��=2sin��·cos��=(2)
|
−
−
−
|
|
cos2��=cos2��−sin2��=(3)
|
−
−
−
|
|
tan2��==(4)
|
4
−4
−
|
|
�y���Q�z
�@<��<��, sin��=�̂Ƃ��C���̒l�����߂Ă��������D sin 2��, cos 2��, tan 2�� �ɓ�����̂��E�̑I��������I��ł��������D
|
|
|
�@���͑�Q�ی��̊p������cos��<0�ɂȂ�C cos��=−=(1) ������ |
−
−
|
|
sin2��=2sin��·cos��=(2)
|
− − |
|
cos2��=cos2��−sin2��=(3)
|
−
−
|
|
tan2��==(4)
|
3
−3
−
|
|
�y���R�z
�@sin67.5���̒l�����߂Ă��������D �ɓ�����̂��E�̑I��������I��ł��������D
|
|
|
sin267.5��==(1) |
−
−
|
|
sin67.5��>0������Csin67.5��=(2)
|
− − |
|
�y���S�z
�@0<��<90��, cos��=�̂Ƃ�sin�l�����߂Ă��������D �ɓ�����̂��E�̑I��������I��ł��������D
|
|
|
sin2==(1) |
−
−
|
|
0��<<45��, sin>0������Csin=(2)
|
− − |
|
�y���T�z
�@<��<��, sin��=�̂Ƃ�cos�l�����߂Ă��������D �ɓ�����̂��E�̑I��������I��ł��������D
|
|
|
<��<��, cos��<0������cos��=(1)
|
−
−
|
|
cos2==(2)
|
− − |
|
<<, cos>0�ɂ��cos=(3)
|
− − |
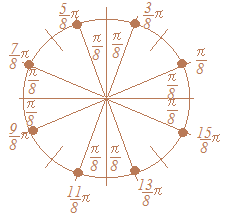 67.5���̏ꍇ��135���̔����Ƃ������Ƃ��g���āC���p��������O�p���̒l�����߂邱�Ƃ��ł��܂����C�E�}�̂悤��
67.5���̏ꍇ��135���̔����Ƃ������Ƃ��g���āC���p��������O�p���̒l�����߂邱�Ƃ��ł��܂����C�E�}�̂悤��