|
■解説 ※定数項や1次式,2次式など単項式や多項式で表わされる式を整式という.
【 要約 】
(証明)整式 A を 整式 B で割ると,商が Q 余りが R になるとき, (1) A÷B=Q … R ⇔ A=BQ+R (2) 余り R の次数は,割る式 B の次数よりも低い. ( B が1次 → R は定数) ( B が2次 → R は1次,定数) ( B が3次 → R は2次,1次,定数) A÷B=Q … R のとき, (1) 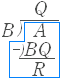 A=BQ+R が成り立つ.(余りはかけ算に参加しない.) (2) 数の割り算では,割る数が取り除ける限り取り除くので,余りは割る数よりも小さい. 多項式の割り算では,割る式よりも次数が低くなるまで取り除くので,余りは割る式よりも次数が低い. (蛇足)・・・割り算が何段階かに分けて行われるときも,上の説明でよい・・・ 数の割り算でも,多項式の割り算でも上の□のように1段階で終わることは少なく,通常次のように,何段階かに分かれる. |
数の割り算の場合
 (1) 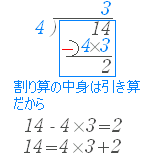 |
| 例1 整式 A を x2+1 で割ると,商が 2x - 1 余りが x+3 になるとき,整式 A を求めよ. (答案) A=(x2+1)(2x - 1)+(x+3)=2x3 - x2+3x+2 …(答) |
例2 整式 x3+x2 - x+2 を整式 B で割ると,商が x - 1 余りが 2x+1 になるとき,整式 B を求めよ. (答案) x3+x2 - x+2=B (x - 1)+(2x+1) B (x - 1)=x3+x2 - x+2 -(2x+1)=x3+x2 - 3x+1 B=(x3+x2 - 3x+1)÷(x - 1)=x2+2x - 1 …(答)
#危険な落とし穴#
A÷B=Q … R であっても A÷Q=B … R とはならないことに注意(この問題では,Q:1次式で割って,余りが1次式となることはない.) したがって, x3+x2 - x+2 を x - 1 で割っても,求めるものは得られない. |
