| (1) 下図のような街路において, A 地点から B 地点まで遠回りせずに行くとき,途中,P 地点も Q 地点も通る道順は何通りあるか. 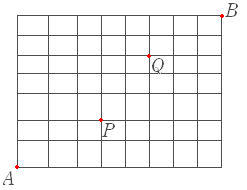 1. 100 通り |
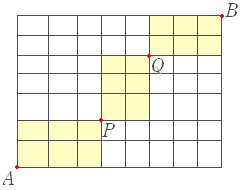 その各々について P 地点から Q 地点まで:5C3==10 通り その各々について Q 地点から B 地点まで:5C2==10 通り 積の法則により,10×10×10=1000 通り(答) |
| (2) (1)と同じ図で P 地点を通り Q 地点を通らない道順は何通りあるか. 1. 760 通り |
A → P の道順 :=10 通り P → B の道順 : 全部で =252 通り そのうち Q 地点を通る道順 :100 通り P 地点から B 地点に行く道順は 152 通り 積の法則により 10×152=1520 通り(答) |
| (3) 次の図において,自動車で A 地点から B 地点まで遠回りせずに行く.図中赤で示した区間は南行き一方通行で,青で示した区間は西行き一方通行のとき道順は何通りあるか. 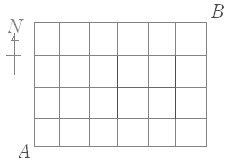 1. 77 通り |
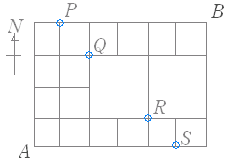 関所 P , Q , R , S を通る道順は P :5 通り Q :10×5=50 通り R :5×(3+1)=20 通り S :2 通り 和の法則により,77 通り(答) |
| (4) 次の図において,P , Q , R の交差点が右折禁止になっているとき,A 地点から B 地点まで遠回りせずに自動車で行く道順は何通りあるか.  1. 40 通り |
A 地点から B 地点まで遠回りせずに行く道順は全部で ○ そのうちで,P の交差点で右折するのは次のような道順で, 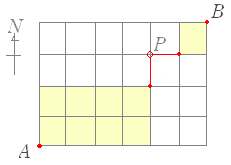 =30 通り ○ 同様にして,Q の交差点で右折するのは, ○ 同様にして,R の交差点で右折するのは, これらの道順には重複はないから,P , Q , R のどれかの交差点で右折する道順は,和の法則により 30+15+4=49 通り 求める道順は 210 - 49=161 通り(答) |
| (5) 次の図において,A 地点から B 地点まで遠回りせずに行く道順は何通りあるか. 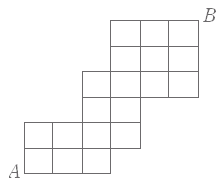
|
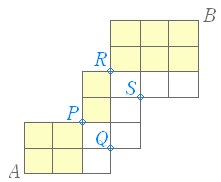 例えば,第1グループPの関所と第2グループRの関所を通る道順は,図の黄色の部分を通る.その道順は 同様にして,P,Sを通る道順は, 同様にして,Q,Rを通る道順は, 同様にして,Q,Sを通る道順は, 合計を和の法則で求めて,520 通り(答) |
