|
(1) 3x−y+1≧0 , x−2y−3≦0 , 2x+y−11≦0 のとき，y−2x の最大値と最小値を求めよ．（正しいものを次の選択肢から選べ．） １． 最大値 4 , 最小値 - 1 |
【 k が切片を表わす場合】
○ 3x−y+1≧0 ⇔ y≦3x+1x−2y−3≦0 ⇔ y≧(x−3) 2x+y−11≦0 ⇔ y≦- 2x+11 の表わす領域は右図の三角形の内部及び周上で， 三角形の頂点の座標は (−1 ,−2 ) , (2 , 7) , (5 , 1) ○ y−2x=k とおくと，y=2x+k の k の値は，ｙ切片を表わす． ○ 右の領域内で y=2x+k の直線（傾き２の直線）を描くと，k の値は，(2 , 7) において最大となり，(5 , 1) において最小となる．（最大値や最小値の値は図で見るよりは，y−2x に代入して求めるとよい．） (2 , 7) のとき，最大値 k=y−2x=7−4 =3 (5 , 1) のとき，最小値 k=y−2x=1−10=−9 |
| (2) 前問(1)と同じ領域において，x−y の最大値と最小値を求めよ．（正しいものを次の選択肢から選べ．） １． 最大値 1 , 最小値 - 5 |
【 切片が大きくなれば k が小さくなる場合】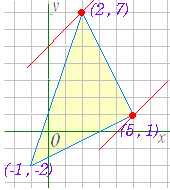
○ x−y=k とおくと，y=x−k において，ｙ切片が大きくなれば k の値は小さくなり，ｙ切片が小さくなれば k の値は大きくなる．○ 傾き１の直線を描くと (5 , 1) のとき， 最大値 k=x−y=5−1= 4 (2 , 7) のとき， 最小値 k=x−y=2−7=−5 |
| (3) x2+y2≦4 のとき，3x−4y の取りうる値の範囲を求めよ．（正しいものを次の選択肢から選べ．） １． −2≦x≦2 |
【 境界線が円の場合】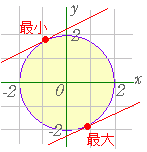
○ x2+y2≦4 の表わす範囲は右図のように円の内部及び周上．3x−4y=k すなわち y=x− とおくと，k の値は傾き の直線のうち，円に接するときに最大及び最小となる． ○ 3x−4y=k が x2+y2=4 に接するときの k の値を求める． ○ （直線が円に接する条件は，連立方程式から一文字を消去して，判別式＝0 の条件で求めることができる．（その方法では接点の座標も求まる．） しかし，ここではもっと計算が簡単な「点と直線の距離」の公式を用いる方法で行ってみる．接点の座標は求まらないが計算は簡単になる．） 点 (p , q) と直線 ax+by+c=0 の距離の公式 を用いて，円の中心 (0 , 0) から直線 3x−4y−k=0 までの距離が 2 となるような k の値を求めると =2 より |k|=10 すなわち k=±10 最大値 k=10，最小値 k=−10 |
| (4) x≧2 , y≧0 , 2x+y≦6 のとき，x2+y2 の最大値と最小値を求めよ．（正しいものを次の選択肢から選べ．） １． 最大値 3 , 最小値 2 |
【 k が円の半径（の２乗）を表わす場合】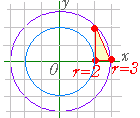
○ x≧2 , y≧0 , 2x+y≦6 は右図のような三角形の内部及び周上○ x2+y2=k とおくと，k は原点を中心とする円の半径の２乗を表わす． ○ 半径の大きさを調べると， 点 (2 , 0) で半径は最小となり，x2+y2=k=4 点 (3 , 0) と (2 , 2) のどちらが大きいかは図だけでは分からないが代入してみれば分かる． (3 , 0) → x2+y2=k=9 (2 , 2) → x2+y2=k=8 よって，(3 , 0) において最大値 9 をとる． |
| (5) x2+y2≦1 のとき，x2+y2−4x の最大値と最小値を求めよ．（正しいものを次の選択肢から選べ．） １． 最大値 3 , 最小値 −1 |
【 k が距離（の２乗）を表わす場合】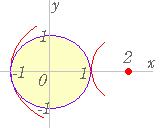
○ x2+y2≦1 の表わす領域は，原点を中心とする半径１の円の内部及び周上．○ x2+y2−4x=k とおくと， (x−2)2+y2=k+4 だから k+4 は点 (2 , 0) を中心とする円の半径の２乗 （点 (2 , 0) からの距離の２乗） 図のように半径は 1≦r≦3 だから 1≦k+4≦9 |
|
(6) x≧1 , y≧1 , x+y≦4 のとき，xy の取り得る値の範囲を求めよ．（正しいものを次の選択肢から選べ．） １． 1≦x≦3 |
【 k が反比例の比例定数を表わす場合】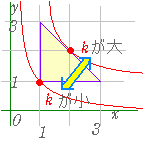
○ x≧1 , y≧1 , x+y≦4 の表わす領域は右図のような三角形の内部及び周上．○ xy=k すなわち，y= とおくと，k は，反比例の比例定数を表わす． (1 , 1) において最小値 xy=k=1 をとる． (2 , 2) において最大値 xy=k=4 をとる． |
| (7) 1≦x+y≦5 , 1≦x−y≦3 のとき，xy−3x の取り得る値の範囲を求めよ．（正しいものを次の選択肢から選べ．） １． −9≦x≦−3 |
【 k が反比例の比例定数を表わす場合】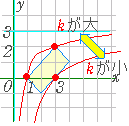
○ 1≦x+y≦5 , 1≦x−y≦3 の表わす領域は右図のような四角形の内部及び周上○ xy−3x=k とおくと， x(y−3)=k → y−3= → y=+3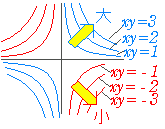 
○ x=0 , y=3 を漸近線とする直角双曲線でこの領域を通るもののうち(1 , 0) , (3 , 2) で最大値をとる． → xy−3x=k=−3 (3 , 0) で最小値をとる． → xy−3x=k=−9 |
| (8) 4≦x+y≦6 , 0≦y−x≦2 のとき， の最大値と最小値を 求めよ．（正しいものを次の選択肢から選べ．） １． 最大値 2 , 最小値 1 |
【 k が比例定数を表わす場合】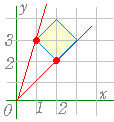
○ 4≦x+y≦6 , 0≦y−x≦2 の表わす領域は右図のような四角形の内部及び周上○ =k とおくと， y=kx の k の値は原点を通る直線の傾きになる． ○ 原点を通る直線の傾きは (1 , 3) で最大値 3 となる． (2 , 2) , (3 , 3) で最小値 1 となる． |
| (9) 3x−y+2≧0 , x+y−2≦0 , x−3y−2≦0 のとき， の最大値と最小値を求めよ．（正しいものを次の選択肢から選べ．） １． 最大値 0 , 最小値 −1   お疲れさまでした．写真は北野天満宮 |
【 k が直線の傾きを表わす場合】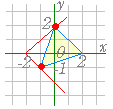
○ 3x−y+2≧0 , x+y−2≦0 , x−3y−2≦0 の表わす領域は右図のような三角形の内部及び周上○ =k とおくと， y=k(x+2) の k の値は (−2 , 0) を通る直線の傾きになる． ○ (−2 , 0) を通る直線の傾きは (0 , 2) で最大値 1 となる． (−1 ,−1) で最小値 −1 となる． |