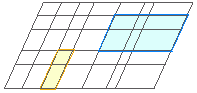
| (1) 正12角形の頂点を結んでできる三角形の総数を m とし,対角線の総数を n とするとき,m , n の組合せとして正しいのはどれか. 1. m=15 , n=12 |
【組合せ】
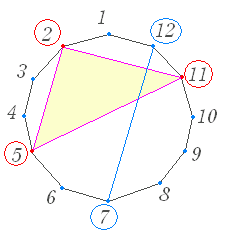 12C3==220 上の図で青の○を付けたものは,頂点を2つ選んだ例で,このように2つの頂点を決めるとそれらを結ぶ対角線が1つ決まる.ただし,これらの中には「対角線」でなく「辺」となるものが12個含まれている(1と2,2と3の組など隣り合うものを選んだ場合)のでこれを引く 12C2−12==54 |
| (2) 次の図のように6本の平行線と8本の平行線が交わっているとき,この図の中に平行四辺形は何個できるか.(例:図中黄色及び青で示したような図形も各々1個の平行四辺形と数える.)
1. 35 |
【組合せ】
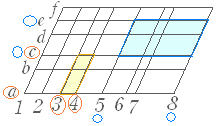 例えば,上の図において黄色の平行四辺形は,横線 a〜 f から2本(a と c )を選び,斜め線 1〜 8 から2本(3 と 4 )を選んだ場合の図形となっている.青の平行四辺形は各々c と e, 5 と 8 を選んだ場合の図形. そこで,総数を求めると 横線の選び方は 6C2==15 通り 斜め線の選び方は 8C2==28 通り 平行四辺形の総数は 15×28=420 |
| (3) 360 の正の約数(1 及び 360 を含む)の個数を m,それらの総和を n とすると,m , n の値は次のうちどれか. 1. m=9 , n=719 |
【積の法則】
《約数の個数と総和》
360=23325 だから,○ p , q , r , ... を素数とするとき,N=paqbrc... と素因数分解される整数 N の約数の個数は (a+1)(b+1)(c+1)··· ○約数の総和は (1+p+p2+···+pa)(1+q+q2+···+qb)(1+r+r2+···+rc)(···) ※この式を展開したとき,すべての項が1回ずつ登場する. その約数の個数は (3+1)(2+1)(1+1)=24 個, 約数の総和は (1+2+4+8)(1+3+9)(1+5)=1170 |
| (4) 1組のトランプの絵札12枚から,種類も数字も異なる3枚のカードを選ぶ方法を m 通りとし,それらを1列に並べる方法を n 通りとすると,m , n の値は次のうちどれか. 1. m=12 , n=72 |
【積の法則】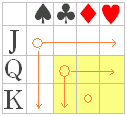 ○1列に並べる方法 n を調べると, ○1列に並べる方法 n を調べると,1枚目はどれでもよいから12通り. その各々について,2枚目は種類も数字も異なるカードから取るから,取り方は6通り. その各々について,3枚目は前2枚と種類も数字も異なるカードから取るから,取り方は2通り. n=12×6×2=144 ○異なる3枚のカードの並べ方 n は,選び方 m の3! 倍あるから,m=n÷3!=24 |
| (5) 4桁の電話番号の千,百,十,一の位の数を各々 a , b , c , d とするとき,9742 のように a>b>c>d となるもの,9774 のように a≧b≧c≧d となるものは各々何通りあるか. 1. 90 通り,810 通り |
【組合せ,重複組合せ】 ○異なる4個の数字を選べば,並べ方は決まる→順序が決められている順列=組合せ 10C4=210 ○重複を許して4個の数字を選べば,並べ方は決まる→重複組合せ 10H4=13C4=715 |
| (6) x+y+x+w=14 (x , y , z , w≧1)を見たす整数解 (x , y , z , w)の個数を求めよ.また,小,中,大,特大の4個のさいころを投げたとき出る目の和が 14 となる場合の数を求めよ. 1. 286 通り,146 通り |
【重複組合せ,場合の数】 ○14個のボールを x , y , z , w≧1 となるように分けるには,初めに1個ずつ渡しておき,残り10個を分ければよい. 4人に重複を許して10個のボールを分ける方法を求めると,4H10=13C10=286 ○上記の解には x=11 , y=1 , z=1 , w=1 のように x , y , z , w>6 となるものも含まれているので,さいころの場合にそのまま適用することはできない. 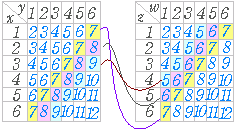 同様にして, x+y=2 , z+w=12 → 1×1=1通り x+y=3 , z+w=11 → 2×2=4通り x+y=4 , z+w=10 → 3×3=9通り ・・・ x+y=7 , z+w=7 → 6×6=36通り ・・・ x+y=12 , z+w=2 → 1×1=1通り 全部で 1+4+9+16+25+36+25+16+9+4+1=146 通り |
| (7) (x2−2x+ )7 の展開式における x 5 の係数を求めよ. 1. 93   お疲れさまでした 写真は京都御苑 |
【多項定理】
(a+b+c)n の展開式における apbqcr の係数は
( ただし,p , q , r≧0 , p+q+r=n )
(証明) ○最近の高校の教科書では,二項定理を何回も適用して説明することが多い. ((a+b)+c)n の展開式における (a+b)n−rcr の係数は nCr (a+b)n−r の展開式における apbq の係数は n−rCq だから結局,n−rCq nCr== ここで,n−q−r=p だから (※同じものがあるときの順列の総数を用いて直接示すこともできる) (x2−2x+)7 の展開式の一般項は (x2)p (−2x)q ()r=(−2)q 3r x2p+q−r だから 2p+q−r=5 …(1), p+q+r=7 …(2), p,q,r≧0 を解く. (1)+(2)より 3p+2q=12 だから p≦4 また 3p=2(6−q) だから p は偶数 → p=0,2,4 (ここまで絞れなくても,p=1,3 のとき,q,r が整数にならないので自然に分かる.解くと言うよりは,順に代入していくと考えるとよい.) ア) p=0 のとき,q=6 , r=1 このとき係数は (−2)6 31=1344 イ) p=2 のとき,q=3 , r=2 このとき係数は (−2)3 32=−15120 ウ) p=4 のとき,q=0 , r=3 このとき係数は (−2)0 33=945 合計 −12831 |