| ※以下は３桁の場合について解説するが，他の場合も同様．負の数，小数，分数も定義できるが，ここでは基本として正の整数のみを扱う． ■ｎ進法とは
正の整数 n（≧2）について，0≦a , b , c≦n - 1 となる整数 a , b , c を用いて
|
例1 3×102+4×10+5 は 10 進法で 345 と書く． 例2 1×22+1×2+0 は 2 進法で 110 と書く． （これは 10 進法の 6 に等しい．） 例3 2×82+0×8+1 は 8 進法で 201 と書く． （これは 10 進法の 129 に等しい．） ※文脈から何進法で書かれたものか分かるときはそのまま書けばよいが，紛らわしいときは，２進法の数は 1101(2) ，３進法の数は 1201(3) などと書けばよい． |
| ■ｎ進法で表わすときの各位の数
ｎ進法では，ｎになると位が上がるので，各位の数にｎ以上の数は使わず 0〜n - 1 までの数を使って表わす．
ただし，最高位の数（先頭）が 0 のときは，桁数が減るので通常は最高位の数は 0 以外と考えてよい． |
例1 10進法では，0〜9 までの数を使って表わす． ３桁の数を abc と書くとき，1≦a ≦9 , 0≦b , c≦9 となる． 例2 ２進法では，0〜1 までの数を使って表わす． ３桁の数を abc と書くとき，a=1 , 0≦b , c≦1 となる． 例3 ８進法では，0〜7 までの数を使って表わす． ３桁の数を abc と書くとき，1≦a ≦7 , 0≦b , c≦7 となる． 例4 16進法では，1つの数で 10〜15 を表わすために a〜f を用い， 0〜15 までの数を 0〜f を使って表わす． ３桁の数を pqr と書くとき，1≦p≦f , 0≦q , r≦f となる． |
| ■ｎ進法で表わされた数を10進法で表わすには
ｎ進法で書かれた数 abc を10進法に直すには
|
例1 ７進法の 123 を 10 進法に直すと 1×72+2×7+3=66 例2 ２進法の 1101 を 10 進法に直すと |
| ■10進法で表わされた数 X をｎ進法で表わすには X=a×n2+b×n+c となる整数 0≦a , b , c≦n - 1 を求めればよいが，これには通常次のような方法が用いられる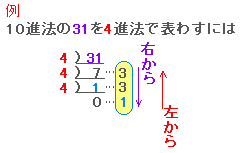．  ※割り算の裏向きのようなこの形の解説が多いが，この方法では末尾の桁から順に求まっている点に注意．ｎ進数の定義に当てはめて，横書きのまま，上から順に求めるには右のようにすればよい． |
（解説） X=(a×n+b)n+c と書けるから， ○X をｎで割ったときの余りが c となる･･･末尾の位（右端）は c ○次に商 a×n+b をｎで割ったときの余りが b となる･･･次に大きな位は b ○２回目の割り算では，商は a となっているから，この商をｎで割った余りは a となる ･･･最高位の数は a （ここで商が0になるので止める） ｎ進法での表記 abc が求まった． （横書きで定義に忠実に行うには） 43=64 , 42=16 , 41=4 , 40=1 を考えておく． 31 の中に 64 は入らないから 16 から考える． 31 から 16 を取れるだけ取ると 1 回取れて，余りは 15 15 から 4 を取れるだけ取ると 3 回取れて，余りは 3 3 から 1 を取れるだけ取ると 3 回取れて，余りは 0 ４進法での表記 133 が求まった． |
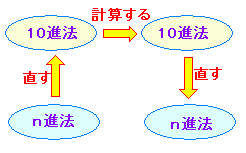 ■ｎ進法で表わされた数の和差積商を求めるには(1) 図のように10進法を経由して行えば確実にできる． 例 ２進法で 1101+1011 の和を求めよ．（結果は２進法で表せ） 答 1101(2)+1011(2)=13+11=24 24=1·16+1·8+0·4+0·2+0=11000(2) |
 (2) 慣れてくれば右のように直接計算してもよい．（ｎ進法ではｎになれば位が上がる点が10進法の計算と異なっている．）
|