|
散布図,相関表,相関係数 ■散布図
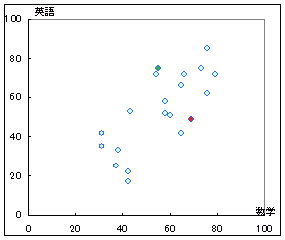
この2種類の数値(数学の得点と英語の得点)の間にとのような関係があるのかを調べるときに,右図1のように数学の得点をx座標に,英語の得点をy座標にして一人ずつを点で表したものを散布図といいます.
散布図に表示すると,2つの量の関係が視覚的にわかりやすくなります.例えば,このデータについては,数学の得点の高い生徒は英語の得点も高い傾向があるといえます.ただし,全くの比例関係ではなく,赤で示した生徒のように数学はそこそこ高いが英語は中位の場合や,緑で示した生徒のように数学は中位でも英語の得点は高いといった場合があるということもわかります.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
【Excelで散布図を作る方法】
上の表1のデータがExcelのワークシート上のA1〜C21に書かれているとし,それを図1のような散布図にするには
各自で練習するときは,上の表を画面上でドラッグ&コピーして,Excel上に単純に貼り付けてください.
(1) 行見出し(数学,英語の欄),列見出し(生徒番号のNo.1〜No.20の欄)を除いて,数字の欄(B2のセルからC21のセルまで)を選択して反転表示にします.(2) Excel2002,Excel2007のいずれでも:挿入→グラフ→散布図(平滑線や折れ線の付いていないものを選ぶ)→完了またはOK (3) 点(マーカー)の色,形,大きさなどはデータ系列の書式設定で変更できます.
なお,個別にマーカーをクリックするとそのデータのx座標とy座標が示されます.これらをデータラベルとして表示することはできますが,あまりスマートなものではありません.
また,普通にインストールされたExcelでは,どの点がどの生徒を表しているかを示すラベル(表1の生徒番号:No.**)をグラフに表示することはできません.どうしてもこれを付けたいときは,マイクロソフト社のWebサイトに紹介されているマクロを組み込む必要があります. |
【問題1】
Excelを使って,右の表2に示されるデータを散布図にしたとき,次のどのグラフになりますか.(転記するのは大変ですので,画面上でドラッグ&コピーし,Excelのワークシート上に単純に貼り付けて使ってください.) 1  2
2 3 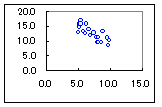 4
4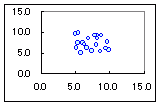 HELP
表だけではわかりにくいですが,実際に散布図にしてみるとわかります.
→3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
【Excelを使って層別散布図(複数系列散布図)を作る方法】
Excelを使って層別散布図(複数系列散布図=右の表で組別にマーカーを区別した散布図)を作るには,あらかじめ表3のようにデータの形を整えておきます. (*) x座標に使う方の数値(右の例では数学)は,どの組にも共通に1つの列に並べます. (**) y座標に使う方の数値(右の例では英語)は,組によって列を変えます.
右の例ではA組が終わってからB組が登場しますが,散布図としてグラフ化するときに重要なのは,違う列に書かれているかどうかで,実際のデータはA組とB組が入り混じって登場しても構いません.ただし,データが途切れてはいけません.
(1) 右の表3のデータが行見出し(数学,英語A組,英語B組)も含めてワークシートのA1からC21に書かれているとします.
右の表3は,ホームページ上で表の枠が正常に表示されるように空白セルに「全角スペースの文字」が入力されています.このデータをそのままコピー・貼り付けしても,このような文字が含まれていると散布図は表示されません.
(2) A1からC21まで行見出しの数学も含めてデータの範囲全部を選択して反転表示にします.(3) Excel2002,Excel2007のいずれでも:挿入→グラフ→散布図(平滑線や折れ線の付いていないものを選ぶ)→完了またはOK (4) 点(マーカー)の色,形,大きさなどはデータ系列の書式設定で変更できます. (結果)⇒ 右図のように表示されます.
【Rコマンダーを使って層別散布図(複数系列散布図)を作る方法】
Rコマンダーを使って層別散布図(複数系列散布図)を作るには,Excel上であらかじめ表4のような形のデータを作っておきます. (*) 層(系列,組分け)の区別は1つの列に文字として書き込みます.この組分けは順不同に入り混じっていても構いません.また,組分けを表す列は左端にあっても右端にあっても構いません. (1) Excel上の書かれた表4のデータを行見出し(数学,英語A組,英語B組)も含めて選択して,コピーします.(クリップボード:メモリに入れます.) (2) RとRコマンダーを起動し,Rコマンダーの中からデータ→データのインポート→テキストファイルまたはクリップボード,URL,...から (3) ファイル内に変数名ありにチェック(数学,英語,組という行見出しを含めたから),クリップボードを選ぶ,区切り文字としてタブを選ぶ(Excelデータをテキストファイルにすると区切り文字としてタブが入るから)→OK (この段階で,データが正しくインポートされたかどうか確かめるために[データセットを表示]のボタンをクリックしてデータを一瞥するとよい) (4) グラフ→散布図→x変数(1つ選択)を数学とする,y変数(1つ選択)を英語とする→周辺箱ひげ図,最小2乗曲線,平滑線のチェックを外す,層別のプロットを選択し層別変数[組],層別して線を描くにチェックが入ったまま→OK (5) OK (結果)⇒ 右図のように表示されます. |
表3の層別散布図 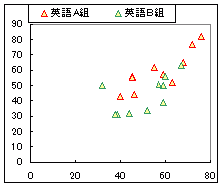 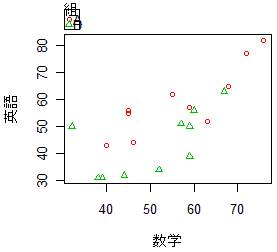 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
【問題2】
Excelを使って,右の表に示されるデータを層別散布図にしたとき,次のどのグラフになりますか. (転記するのは大変ですので,画面上でドラッグ&コピーし,Excelのワークシート上に単純に貼り付けて使ってください.ただし,Webページに表示する都合で空白セルに全角(2バイト文字)スペースが入っています.このままExcelに移すとうまく表示されませんので,Excel上で全角(2バイト文字)スペースをすべて削除してから散布図にしてください.)
1 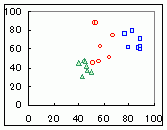 2
2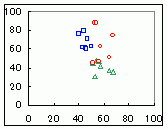 3 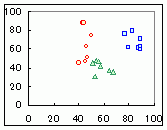 4
4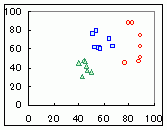 HELP
表だけではわかりにくいですが,実際に散布図にしてみるとわかります.なお,マーカーの色や形は好みに応じて変えられます.
→1
|
|
|
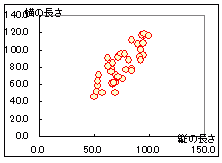
■分割表(相関表)の作成 右の表5のデータを散布図にすると図6のようになりますが,データの個数が多いと互いに重なってしまって見にくくなります. 表6のように縦・横それぞれを適当な区間に区切って度数分布表(の組合せ)にしたものを,相関表(分割表,クロス集計表)といいます. 散布図と相関表にはそれぞれのよさがありますので,利用目的に応じて使い分けるとよいでしょう.
【Excelを使って相関表を作成する方法】
≪全体の流れ≫
表5のデータがワークシートのA1〜B41に書かれているものとします.このデータから,まず[1]ピボットテーブルを作成し,次に[2]グループ化を行うと,相関表ができます.
==Excel2002の場合 ==[1] ……ピボットテーブルの作成……
(1) データの中のどこかをポイントしておき,データ→ピボットテーブルとピボットグラフレポート
[2] ……グループ化……Excelのリスト/データベース,ピボットテーブルが選択された状態で次へ 使用するデータの範囲を指定してください:A1:B41→次へ そのワークシート上にピボットテーブルを作成するときは,既存のワークシートを選び,左端の位置としてD1などと指定→完了 (2) 縦の長さを左の表題の欄(行見出し)までドラッグ,横の長さを上の表題の欄(列見出し)までドラッグ さらに,縦の長さ(横の長さでもよい)をもう一度「ここにデ-タアイテムをドラッグします」という欄にドラッグ (3) そのままでは,数字の合計が計算されているので,左上端のボタンをダブルクリックして「データの個数」を指定します. (4) 以上により,一時的に縦横とも相当大きな表ができます(このままでは,かなり見づらいものです).
(1) ピボットテーブルの行見出しを右クリックし,グループと詳細の表示→グループ化
(2) 先頭の値50,末尾の値100,単位(=これが階級幅になります)10→OK 上端の列見出しについても同様にグループ化します. (結果)⇒ 右の表6のように表示されます. ※ この表では,階級が50-60,60-70のように区切りとなる値が重複して表示されますが,以上のようにピボットテーブルからグループ化した場合,各々50以上-60未満,60以上-70未満を表しています. たとえば,表5の68.7,50.0のデータは,横の長さ40-50の階級ではなく,50-60の階級に入っています. ※ 当然のことですが,このようにして作った相関表では縦の長さは下に進むほど大きくなっているので,散布図とは上下が逆になります. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
【問題3】
Excelを使って,右の表に示されるデータを縦横とも先頭の値20,階級幅10の相関表(分割表)にするものとします.各々の階級は,例えば縦20以上30未満,横20以上30未満となるところを縦20-30,横20-30のように表示するとき,最も度数が多い階級は次のどの階級になりますか.相関表(分割表)を完成させて答えてください. (転記するのは大変ですので,画面上でドラッグ&コピーし,Excelのワークシート上に単純に貼り付けて使ってください.)
1縦20-30,横50-60 2縦40-50,横50-60 3縦30-40,横40-50 4縦30-40,横50-60 HELP
次のような表になります.この表から,最も度数が多い階級は縦30-40,横40-50(赤で示した6)になります.
→3
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

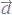 ,
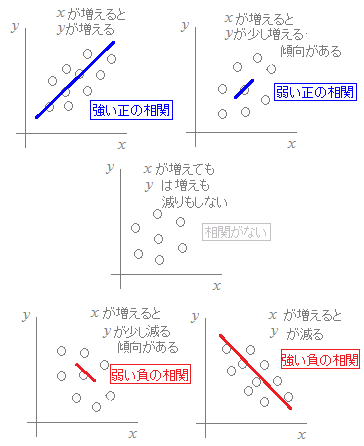
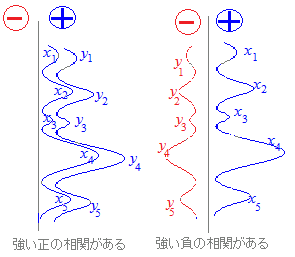
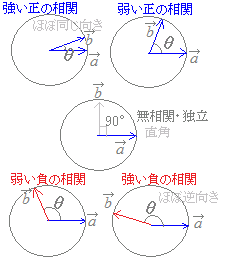
,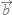 が同じ方向のときにこれらは正の相関があると考え,逆向きのときは負の相関があると考えます.直角のときは一方が増えても,他方は増えも減りもしませんので,無関係とします.
が同じ方向のときにこれらは正の相関があると考え,逆向きのときは負の相関があると考えます.直角のときは一方が増えても,他方は増えも減りもしませんので,無関係とします.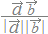
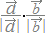 によって計算しましたが,(3)で述べたようにC列とD列の積の和を求めてから,長さの積で割って
によって計算しましたが,(3)で述べたようにC列とD列の積の和を求めてから,長さの積で割って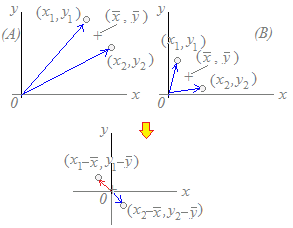
 たとえば,親の身長と子供の身長には相関が強いと言われており,この場合は親の身長と子供の身長には因果関係があると言えるでしょう.(親が原因で子供が結果)
たとえば,親の身長と子供の身長には相関が強いと言われており,この場合は親の身長と子供の身長には因果関係があると言えるでしょう.(親が原因で子供が結果) たとえば,着実な学習習慣のような第3の要因があって,これが満たされているから数学も英語もよくできるというのならば納得のいく説明になります.
たとえば,着実な学習習慣のような第3の要因があって,これが満たされているから数学も英語もよくできるというのならば納得のいく説明になります.