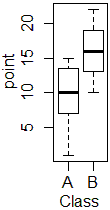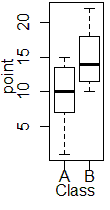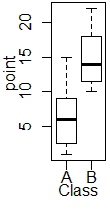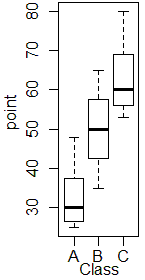|
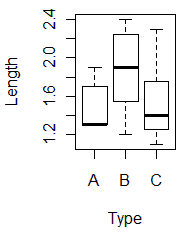
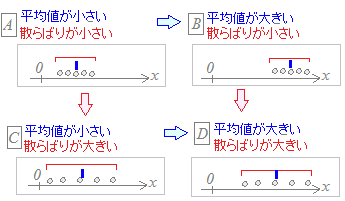
■データの散布度(散らばり) 平均値が等しくてもデータの分布の様子が違う場合があります. 右図のAとC,BとDでは平均値が同じですが,散らばりが異なります.また,AとB,CとDでは散らばりが同じですが,平均値が異なります. このように,データの分布の様子をとらえるためには,中心付近がどこにあるかを示す平均値だけでなく,散らばり具合を表す数値もしばしば併用されます.
■範囲(レンジ)==-散らばりを表す方法(その1)===
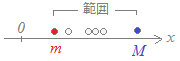
散らばり具合を表す簡単な数値は,最大値Mと最小値mの差で定義される「範囲(レンジ)」です. 範囲=M−m
範囲が大きいほど,広く散らばっていると言えます.
Excelで,データが数個の数値からなる場合には,範囲は数値を順に見れば分かりますが,数百〜数千個の数値からなる場合には最大値と最小値をワークシート関数を使って求めることができます.
【例1】 (Excelを使った計算)
右の表1のデータがExcelワークシートのA1〜B10にあるとき,
最大値は =MAX(A1:B10) (結果は4.7)
で求めることができます.(コンピュータの標準的なデータは,1列または1行に格納されたデータを取り扱いますが,表計算ソフトExcelでは複数の行または列にまたがる長方形に配置されたデータについても,=Max()や=MIN()を使うことができます.)
最小値は =MIN(A1:B10) (結果は0.1) 範囲は =MAX(A1:B10)−MIN(A1:B10) (結果は4.6)
【問題1】
Excelを使って,右の表2に示されるデータの範囲を求めてください.(転記するのは大変ですので,画面上でドラッグ&コピーし,Excelのワークシート上に単純に貼り付けて使ってください.) 13.7 24.3 34.5 44.7 HELP
右の表2のデータがExcelワークシートのA1〜E20にあるとき,
最大値は =MAX(A1:E20) (結果は4.6)
で求めることができます.最小値は =MIN(A1:E20) (結果は0.3) 範囲は =MAX(A1:E20)−MIN(A1:E20) (結果は4.3) →2
|
|
|
■四分位数==-散らばりを表す方法(その2)===
データを小さい順に並べたときに4等分する順位の値を四分位数といいます. 四分位数は,データを小さい方から25%となる値:第1四分位数,小さい方から50%となる値:第2四分位数,小さい方から75%となる値:第3四分位数からなり,各々Q1 , Q2 , Q3で表します.
第2四分位数は,データ全体の中央値と同じものです.
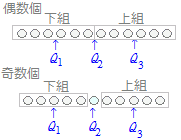 データが偶数個からなるときは,下組の中央値が第1四分位数になり,上組の中央値が第3四分位数になります. データが偶数個からなるときは,下組の中央値が第1四分位数になり,上組の中央値が第3四分位数になります.データが奇数個からなるときは,データ全体の中央値を取り除いた2つの組について,下組の中央値が第1四分位数とし,上組の中央値が第3四分位数とすることになっています. ※四分位数により「データが左右対称かどうか」「外れ値(極端値)があるかどうか」を判断できます.(後述:箱ひげ図によってよく分かります) ○ Excelを使って四分位数を求める方法 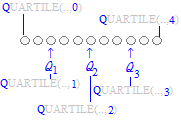 Excelのワークシート関数 =QUARTILE(第1引数, 第2引数) において,第2引数にQ1 , Q2 , Q3の添え字1, 2, 3を指定すると各々の四分位数が返されます.
Excelのワークシート関数 =QUARTILE(第1引数, 第2引数) において,第2引数にQ1 , Q2 , Q3の添え字1, 2, 3を指定すると各々の四分位数が返されます.さらに,第2引数に0を指定すると最小値,4を指定すると最大値が返されます. ただし,四分位数には幾つか異なる定義があり,高校の教科書の定義とExcelに使われている定義とでは,第2四分位数は一致しますが,第1四分位数,第3四分位数は必ずしも一致しません.(データの個数が多くなるとこの差異は無視できる程度に微小なものとなります.) 高校の教科書の定義に従った四分位数をExcelを使って求めるには,
○ 第2四分位数は,データ全体の中央値と一致しますので =MEDIAN() で求めることができます.
○ 第1四分位数と第3四分位数を求めるためには,あらかじめデータを昇順にソート(並べ替え)しておき,
偶数個ならば,そのまま下組の中央値を=MEDIAN()で求める.
奇数個ならば,全体の中央値を除いた上組と下組の各々について=MEDIAN()を求める.
【例2】 (Excelを使った計算)・・・ただし,四分位数の定義は高校の教科書による
右の表3のデータがワークシートのA1〜A21にあるとき
最小値は =MIN(A1:A21) (結果は2.1)
で求めることができます.
第2四分位数は =MEDIAN(A1:A21) (結果は3.8) 次に,データが奇数個(21個)なので,中央値を除いた20個の数値について,上組と下組を作ります. 第1四分位数を求めるには,データをソートしてから中央値を除いた下組10個について =MEDIAN(A1:A10) (結果は2.65) 第3四分位数は中央値を除いた下組10個について =MEDIAN(A12:A21) (結果は4.25) 最大値は =MAX(A1:A21) (結果は5.8) |
≪高校の教科書とExcelの=QUARTILE()の違い:図解≫
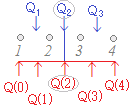 ■高校の教科書:下組(上組)の「値」の中央値が第1(3)四分位数
■高校の教科書:下組(上組)の「値」の中央値が第1(3)四分位数■Excelの=QUARTILE():下組(上組)を実数軸上に並べたときの25%(75%)の場所が表す数値を比例配分で求めたものが第1(3)四分位数 【例A】 右の例:1,2,3,4の場合
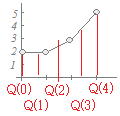 【例B】 右の例:2,2,3,5の場合
【例B】 右の例:2,2,3,5の場合
【問題2】
高校数学Iの教科書の定義に従って,右の表4に示されるデータの四分位数を求めてください. 1Q1=2 , Q2 =4.5 , Q3=7 2Q1=2.5 , Q2 =4.5 , Q3=7.5 3Q1=2 , Q2 =5 , Q3=7 4Q1=2 , Q2 =5 , Q3=7.5 5Q1=2.5 , Q2 =5 , Q3=7.5 HELP
中央値はQ2=5
次に,データが奇数個だから中央値を除いて下組{1,2,2,4}と上組{6,7,8,9}を考え,各々について中央値を調べると Q1=2, Q3=7.5 →4
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
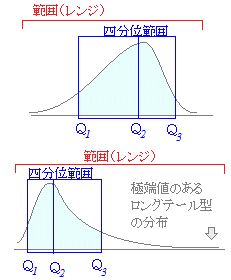 ■四分位範囲 ■四分位範囲第3四分位数と第1四分位数との差 Q3−Q1 を四分位範囲といいます. 前に述べた「範囲(レンジ)」は,最大値から最小値までの幅で定義されますので,極端値(外れ値)があるときにその影響を受けやすくなります. これに対して,「四分位範囲」は多くの場合,右図のように社会現象でよく表れるロングテール型の分布においても,極端値を除いたデータの主要部分のある範囲を表します. |
まず,中央値を求める:(偶数個だから7と7の平均)7
次に,下組の中央値はQ1=4,上組の中央値はQ3=8.5 四分位範囲はQ3−Q1=4.5 →3
|
|
■箱ひげ図
Excelを使って箱ひげ図を作成する方法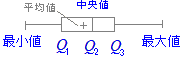 最小値,第1四分位数,第2四分位数(=中央値),第3四分位数,最大値を右図のように表したものを「箱ひげ図」といいます. 最小値,第1四分位数,第2四分位数(=中央値),第3四分位数,最大値を右図のように表したものを「箱ひげ図」といいます.
平均値は中央値とは別のものです.箱ひげ図に平均値を+記号で示す場合もありますが,これは書かないこともあります.
箱ひげ図を使えば
・左右対称かどうか
などが一目でわかります.
・データの主要部分はどの辺りにあるか ・極端値があるかどうか
Excel2002〜2007の標準機能としては,箱ひげ図のグラフを作成することはできないようです.ここでは,Excelのフリーのアドインソフト,RとRコマンダーを使って,箱ひげ図を作成する方法を解説します.
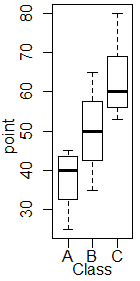
層別(A,B,Cという種類別の)箱ひげ図というものを作成するためには,右の表6の形式でデータを準備します.(並べ方は適当でいいですが,種類別に箱ひげ図を作るには数値の欄以外に種類を表す文字が必要です.)RとRコマンダーのインストール方法は,この頁に解説があります. ≪手順≫ (1) Excelの中からRコマンダーを起動しておきます. (2) Excelで表6の形式でデータを準備し,データの範囲をコピーしてクリップボード(メモリ)に入れます. (3) Rコマンダーのメニューで,データ→データのインポート→テキストファイルまたはクリップボード...から 「ファイル内に変数名あり」にチェック,「クリップボード」,フィールドの区切り記号は「タブ」→OK (4) データが正しくインポートされたかどうか[データセットを表示]のボタンを押す (5) グラフ→箱ひげ図→層別のプロット→OK,OK (6) 右図1の箱ひげ図ができます.
※1 Rコマンダーで箱ひげ図を作るには,最小値,第1四分位数,第2四分位数(=中央値),第3四分位数,最大値を入力する必要はなく,データを示せば後は自動的に作成されます.(ただし,四分位数の定義はExcelの定義と同様になります)
Rコマンダーの箱ひげ図では,極端値(外れ値)は※2 図1のType Cの箱ひげ図を見ると,最大値が第3四分数から離れたところにあることが分かります.また,Type Cは左寄りの分布になっています. ※3 Type Aの箱ひげ図を見ると,最小値が中央値に一致しており,下位グループが濃い,左寄りに分布になっていることがわかります. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
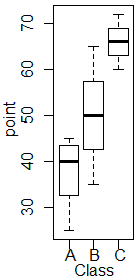
Aは右(上)寄りで左(下)にロングテールになっています.また,Bは左右(上下)対称になっています.
→1
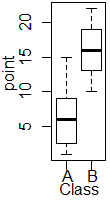
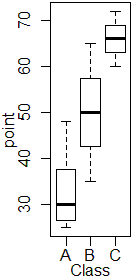
Aは左(下)寄り,Bは左右(上下)対称,Cが左(下)寄りとなっています.
→4
|
|
|
■平均偏差,絶対偏差,標準偏差
データの散らばり具合を表すものとして,ここまでに「範囲」「四分位範囲」が登場しましたが,すべての値を使って詳細に示す数値を考えます.
○ データの各々の値と平均値 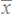 との差 との差xk− 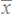 (k=1,2,3,..) (k=1,2,3,..)のことを偏差といいます. ▼ 偏差が大きいほど中心付近から離れているので,この偏差の平均値を求めると,全体の散らばり具合が表せるのではないかと考えてみます.ところが,右図2の例では,x4− 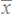 , x5− , x5−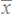 , x6− , x6−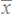 は正の値になりますが,x1− は正の値になりますが,x1−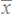 , x2− , x2−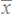 , x3− , x3−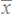 は負の値になって,偏差の平均は0になるため,散らばり具合を表すことができません. は負の値になって,偏差の平均は0になるため,散らばり具合を表すことができません.
【要約】
「平均偏差」はつねに0になるため,散らばり具合を表せない. ▼ そこで,正の値と負の値が打ち消し合わないように,偏差の絶対値|xk− 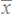 | (k=1,2,3,..)の平均を取ってみます.このようにして定義される「絶対偏差」は確かに散らばり具合をあらわすことができますが,絶対値記号の付いた式は変形しにくく,以後の応用に不便なのであまり使われません. | (k=1,2,3,..)の平均を取ってみます.このようにして定義される「絶対偏差」は確かに散らばり具合をあらわすことができますが,絶対値記号の付いた式は変形しにくく,以後の応用に不便なのであまり使われません.
【要約】
「絶対偏差」は,散らばり具合を表すことができるが,絶対値記号が変形しにくいのであまり使われない. ○ そこで,負の値でも2乗すると正の数に変わることを利用して,偏差の2乗(xk− 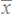 )2 (k=1,2,3,..)がよく使われます. )2 (k=1,2,3,..)がよく使われます.
【偏差2乗和】
(解説)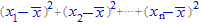 【分散】 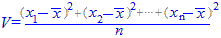 【標準偏差】 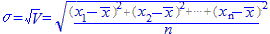 【偏差2乗和】
偏差の2乗を足したもので,データ全体で平均値からどれだけズレているかを表すために用いられます.
【分散】
偏差の2乗の平均値のことえお分散といい,よく利用されます.分散は,1個当たりのズレを表しますが,元の変数xk (k=1,2,3,..)とは単位や大きさの尺度が違うことに注意しましょう.(たとえば,元の数値がcm単位であるとき,分散の単位はcm2になります.)
【標準偏差】
分散を元の変数と同じ単位と尺度に直すものとして,標準偏差があります.
右の表9のデータがExcelワークシートのA1からA12にあるとき,○[Excelを使って偏差2乗和を求める方法] 偏差2乗和を求めるためには,まず平均値 =AVERAGE(A1:A12) とします. 次に,個別に偏差を求めます. B1のセルに =A1−$A$14 これをコピーして,B2からB12に貼り付けます.(A14を絶対参照 $A$14 にしておくと,コピー&貼り付けのときに番地がずれるのを防げます.) さらに,それらの2乗を一度求めてから,次の計算に移るのもよい方法ですが,ここでは一気に2乗の和を求める関数 =SUMSQ() (2乗 SQ の和 SUM)を利用してみます. B13のセルに =SUMSQ(B1:B12) ⇒ 以上により,偏差2乗和は 0.986666667 となります.(有効数字を調整するには,書式として表示桁数だけを調整し,実際の数値は変えないようにします) |
図2
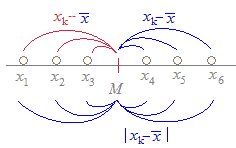 平均偏差=
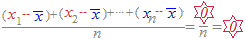 絶対偏差=
※ 絶対値偏差は,Excelのワークシート関数 =AVEDEV() で求めることができます.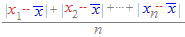
(1) 上記のようにB13に偏差2乗和が求められている場合は, =B13/12 …(1) によって,分散を求めることができます. (2) 上記の手順を踏まずに元のデータA1〜A12から直接に分散を求めるには =VARP(A1:A12) …(2) とします. ⇒ 以上により,分散は 0.082222222 となります.(有効数字を調整するには,書式として表示桁数だけを調整し,実際の数値は変えないようにします)
(2)があれば(1)は不要と考えている人へ
実際の作業では,関数に指定するセル範囲の間違いなど計算間違いにつながる要素はたくさんありますので「異なる求め方で計算して,それらが一致すれば検算になる」と考えるとよいでしょう.
Excelには分散を求めるための関数が2種類用意されていますので,使い方を間違わないように注意しましょう.
○[Excelを使って標準偏差を求める方法]ここでやった例のように,与えあられたデータ自体の分散を求める関数は =VARP() です. これに対して,例えば1000個の母集団から30個の標本を抽出して調べているときに,30個の標本から元の母集団の分散を推測するために使う関数が =VAR() です.(分散を初めて習うときには,このような推測統計の話は登場しません.) (1) 上記の方法でB14に分散が求められている場合は, =SQRT(B14) …(3) によって,分散を求めることができます. (2) 偏差2乗和も分散も経由せずに元のデータから直接に標準偏差を求めるには =STDEVP(A1:A12) …(4) とします. ⇒ 以上により,標準偏差は 0.286744176 となります.
標準偏差についても関数が2種類用意されていますので,使い方を間違わないように注意しましょう.
ここでやった例のように,与えられたデータ自体の標準偏差を求める関数は =STDEVP() です. これに対して,例えば1000個の母集団から30個の標本を抽出して調べているときに,30個の標本から元の母集団の分散を推測するために使う関数が =STDEV() です. |
|||||||||||||||||||||||||||||||||||||||||||||
|
右の表10のデータをExcelワークシートのA1〜A12にコピー&貼り付けして,以下の問題に答えてください.
=AVERAGE(A1:A12)によって平均値を求めると,8.358333333
これが,A14に書かれているとして,=A1−$A$14により偏差を求め,コピー・貼り付け(B1〜B12に求めたとします) 最後に,=SUMSQ(B1:B12)により,偏差2乗和が求まります. (結果は,16.82916667になるので,元の数値が小数第1位までであったのに対して小数第2位まで求めるとよいでしょう) →4
=VARP(A1:A12)により1.402430556となります.
→2
=STDEVP(A1:A12)により1.184242608となります.
→1
|
|