|
→ 携帯用は別頁
【例題1】
(解答)次の関数の増減を調べて極値を求めてください. y=x2−2x+3 y’=2x−2=2(x−1) y’=0 ⇔ x=1
区間x<1で減少,区間x>1で増加…(答) x=1のとき極小値2をとる…(答) |
|
→ 携帯用は別頁
【例題1】
(解答)次の関数の増減を調べて極値を求めてください. y=x2−2x+3 y’=2x−2=2(x−1) y’=0 ⇔ x=1
区間x<1で減少,区間x>1で増加…(答) x=1のとき極小値2をとる…(答) |
|
次の関数の増減を調べて極値を求めてください.
【問題1-2】
採点する
やり直す
解説を読む
y=x3−6x2+9x (略解) x=のとき極大値 x=のとき極小値
(解答)
y’=3x2−12x+9=3(x−1)(x−3) y’=0 ⇔ x=1, 3
区間1<x<3で減少,区間x<1, x>3で増加 x=1のとき極大値4,x=3のとき極小値0…(答) |
次の関数の増減を調べて極値を求めてください.
【問題1-3】
採点する
やり直す
解説を読む
y=−2x3+3x2−4 (略解) x=のとき極大値 x=のとき極小値
(解答)
y’=−6x2+6x=−6x(x−1) y’=0 ⇔ x=0, 1
区間x<0, 1<xで減少,区間0<x<1で増加 x=1のとき極大値−3,x=0のとき極小値−4…(答) |
|
【3次関数と極値の有無】
ここでは,a>0の場合を扱う. 3次関数y=ax3+bx2+cx+d…(#1)が極値を持つかどうかを調べたいとき y’=3ax2+2bx+c=0…(#2)とおいた2次方程式の実数解の個数によって,グラフの形は次の3通りに分かれる. 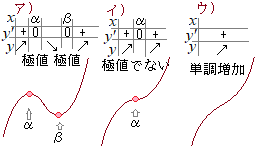 ア) D’>0のとき (#2)の2次方程式は,異なる2つの実数解α, βをもち,(#1)のグラフは,図のア)の形になる.極大値と極小値がある イ) D’=0のとき (#2)の2次方程式は,重解αをもち,(#1)のグラフは,図のイ)の形になる. y’=0となる点が1つx=αだけあるが,その前後で増減は変化しないので,極値はない. ウ) D’<0のとき (#2)の2次方程式は,実数解をもたず,(#1)のグラフは,図のウ)のような「単調増加」になる. |
【例題2】
(解答)次の関数が極値をもたないとき,定数kの値の範囲を求めてください. y=x3+3x2+kx y’=3x2+6x+k y’=0となるxの2次方程式が異なる2つの実数解をもたなければ(重解または虚数解となるとき),元の関数は極値をもたない 判別式D'=9−3k≦0より k≧3…(答) (参考) 下の図で,初めk=1の場合のグラフが描かれています.桃色の縦長のスケールでkの値をクリックすると,それに応じて関数のグラフが描かれます. k=3の前後でグラフがどのように変化するかを観察してください.
kの値
|
|
【問題2-2】
採点する
やり直す
解説を読む
次の関数が極値をもたないように,定数kの値の範囲を求めてください. ≦k≦
(解答)
y’=x2−kx+1 y’=0となるxの2次方程式が重解または異なる2つの実数解をもたないとき,元の関数は極値をもたない 判別式D=k2−4≦0より −2≦k≦2…(答) (参考) 下の図で,初めk=0の場合のグラフが描かれています.桃色の縦長のスケールでkの値をクリックすると,それに応じて関数のグラフが描かれます. k=−2, 2の前後でグラフがどのように変化するかを観察してください.
kの値
|
|
【問題2-3】
採点する
やり直す
解説を読む
次の関数が極値をもつように,定数kの値の範囲を求めてください. y=x3+(k+2)x2+3kx k<,<k
(解答)
y’=3x2+2(k+2)x+3k y’=0となるxの2次方程式が異なる2つの実数解をもつことが極値をもつための条件となる 判別式D'=(k+2)2−9k>0より k2−5k+4>0 (k−1)(k−4)>0 k<1 4<k…(答) (参考) 下の図で,初めk=0の場合のグラフが描かれています.桃色の縦長のスケールでkの値をクリックすると,それに応じて関数のグラフが描かれます. k=1, 4の前後でグラフがどのように変化するかを観察してください.
kの値
|
【絶対値付き関数の極値】
(解説)(1) 元の関数では極値でない点が絶対値付き関数では極値になることがある.これは,絶対値記号によってできる角点(折り目)で起こる. (2) 絶対値付き関数の増減を調べるには,区間を場合分けして増減表を作り,全体をつなぎ合わすのが基本です. ただし,式全体が1つの絶対値記号で囲まれている場合は,「逆さ富士」「鏡写し」の要領でx軸に対称に上下をひっくり返すだけでできる. (3) 角点(折り目)が極値になっている場合は,関数の値(極値)は定義されているが,微分係数は定義されない. 下図①は,y=xおよびy=|x|のグラフです. 下図②は,y=x(x−2)およびy=|x(x−2)|のグラフです. (2)→いずれも,赤色のグラフをx軸に対称に上下をひっくり返したものが青色で示した絶対値付き関数のグラフです. (1)→このようにしてできる絶対値付き関数のブラフは赤丸で示した点が「角点」(=折り目)になっています. (3)→数学Ⅱでは詳しく教えている時間はありませんが「x=αの近傍のどんな値に対してもf(α)≦f(x)が成り立つとき,x=αで極小」と言います.だから,(連続な関数を前提として)微分係数が0にならなくても,減少から増加に変化している点があれば,その点で極小になります. 「x=αの近傍のどんな値に対してもf(α)≧f(x)が成り立つとき,x=αで極大」と言います.だから,(連続な関数を前提として)微分係数が0にならなくても,増加から減少に変化している点があれば,その点で極大になります. 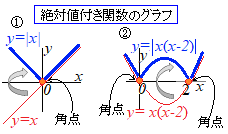
これに対して,x=0, 2の点は微分係数が定義されない.左から近づいたときと右から近づいたときの微分係数が一致しないときは,その点で「微分係数なし」とし,増減表では「×」で示す. x=0, 2の点では微分係数がないが,関数値は定義されており,それぞれ極小値f(0)=0, f(2)=0となる. |
|
【例題3】
(解答)次の関数の増減を調べて極値を求めてください. y=|x|(x−2) 絶対値付き関数の増減を調べるとき,「区間を場合分けして,絶対値を外してから,微分などを行い,増減表を作る」のが基本です. ア) x<0のとき,y=−x(x−2)=−x2+2x y’=−2x+2=−2(x−1) y’=0 ⇔ x=1
イ) 0≦xのとき,y=x(x−2)=x2−2x y’=2x−2=2(x−1) y’=0 ⇔ x=1
ア)イ)の表をつなぎ合わせると
上の増減表により 区間0<x<1で減少,区間x<0, 1<xで増加…(答) x=0のとき極大値0,x=1のとき極小値−1…(答) (参考)グラフは下図のようになります |
• 空欄を「半角数字(1, 2, 3 など)」「半角英小文字」(a, b, c など)で埋めて,採点ボタンを押してください.
• 採点すれば採点結果と解説が出ます.見ているだけでは解説は出ません. |
|
• 空欄を「半角数字(1, 2, 3 など)」「半角英小文字」(a, b, c など)で埋めて,採点ボタンを押してください.
• 採点すれば採点結果と解説が出ます.見ているだけでは解説は出ません.
【問題3-2】
採点する
やり直す
解説を読む
次の関数の極値を求めてください. y=|x(x−3)|+x−1 x=のとき,極大値 ア x=のとき,極小値 イ x=のとき,極小値 ウ (イ<ウとする) |
(解答)
ア) x≦0, 3≦xのとき,y=x(x−3)+x−1=x2−2x−1 y’=2x−2=2(x−1) y’=0 ⇔ x=1(区間外)
イ) 0<x<3のとき,y=−x(x−3)+x−1=−x2+4x−1 y’=−2x+4=−2(x−2) y’=0 ⇔ x=2
ア)イ)の表をつなぎ合わせると
上の増減表により x=2のとき極大値3 x=0のとき極小値−1,x=3のとき極小値2…(答) (参考) • グラフは下図の赤線のようになります. • なお,このグラフはy=x(x−3)のグラフを描いてから,それを「逆さ富士」「鏡写し」の要領でx軸に対称に上下をひっくり返したもの:y=|x(x−3)|(青線のグラフ)を,y=xの直線(灰色のグラフ)の上に乗せてから,y方向に−1だけ平行移動したと考えてもよい. • ややこしい話:角点からなる極小値は上下だけ移動するが,y’=0となる点(極大値)の方は,左右移動も伴うので注意( |