�s�\����������  \( \displaystyle x \) \( \displaystyle x \)�̗ݏ�́C0�ɋ߂����ɂȂ�t
�@�Ⴆ�C
=A_0%2B A_1x%2B A_2x^2%2B a_3x^3%2B\cdots&chco=aa4422) \( \displaystyle f(x)=A_0+ A_1x+ A_2x^2+ a_3x^3+\cdots \) \( \displaystyle f(x)=A_0+ A_1x+ A_2x^2+ a_3x^3+\cdots \)
�ɂ���
 \( \displaystyle A_0=3,\hspace{2px}A_1=1,\hspace{2px}A_2=4,\hspace{2px}\cdots \) \( \displaystyle A_0=3,\hspace{2px}A_1=1,\hspace{2px}A_2=4,\hspace{2px}\cdots \)�C  \( \displaystyle x=0.1 \) \( \displaystyle x=0.1 \)
�̂Ƃ�
=3%2B 1\times 0.1%2B 4\times 0.1^2%2B\cdots&chco=aa4422) \( \displaystyle f(x)=3+ 1\times 0.1+ 4\times 0.1^2+\cdots \) \( \displaystyle f(x)=3+ 1\times 0.1+ 4\times 0.1^2+\cdots \)
 \( \displaystyle =3.14\cdots \) \( \displaystyle =3.14\cdots \)
�̂悤��
 \( \displaystyle x=0.1,\hspace{4px}x^2=0.01,\hspace{4px}x^3=0.001,\cdots \) \( \displaystyle x=0.1,\hspace{4px}x^2=0.01,\hspace{4px}x^3=0.001,\cdots \)
�ƂȂ邩��C  \( \displaystyle x \) \( \displaystyle x \)�̎����̍������͂ǂ�ǂ����Ȃ�D
�@���ɁC���̗�̂悤�ɁC  \( \displaystyle x=0.1 \) \( \displaystyle x=0.1 \)�̂Ƃ��C  \( \displaystyle x^n \) \( \displaystyle x^n \)�͏����� n�ʂ̈ʎ���\���D
�@�l�X�ȏ����v�Z�ɂ����āC�L��������3��������Ώ\���ł��邱�Ƃ���������
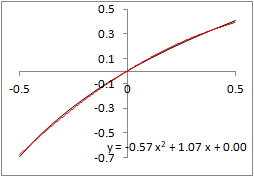
&chco=aa4422) \( \displaystyle f(x) \)�� \( \displaystyle f(x) \)�� \( \displaystyle A_0+ A_1x+ A_2x^2 \) \( \displaystyle A_0+ A_1x+ A_2x^2 \)
�̂悤�ȋߎ����ŏ\���Ȑ��x�������邱�Ƃ������D
�y�v�_2�z�@�Q���̋ߎ���
h��0�̂Ƃ�
) \( \displaystyle f(a+ h) \)�� \( \displaystyle f(a+ h) \)��%2B f\apos(a)h%2B\frac{f\apos\apos(a)}{2}h^2) \( \displaystyle f(a)+ f'(a)h+\frac{f''(a)}{2}h^2 \) \( \displaystyle f(a)+ f'(a)h+\frac{f''(a)}{2}h^2 \)���(3)
x��0�̂Ƃ�
) \( \displaystyle f(x) \)�� \( \displaystyle f(x) \)��%2B f\apos(0)x%2B\frac{f\apos\apos(0)}{2}x^2) \( \displaystyle f(0)+ f'(0)x+\frac{f''(0)}{2}x^2 \) \( \displaystyle f(0)+ f'(0)x+\frac{f''(0)}{2}x^2 \)���(4)
|
�i����j
(3)←
a��萔�Ƃ���Ƃ��C�ϐ�h�̊�f(a+h)��
) \( \displaystyle f(a+h) \)�� \( \displaystyle f(a+h) \)�� \( \displaystyle A_0+ A_1h+ A_2h^2 \)����@ \( \displaystyle A_0+ A_1h+ A_2h^2 \)����@
�̌`�̂Q�����ŋߎ��ł���Ƃ���D�@�̗��ӂ�h�Ŕ��������
) \( \displaystyle f'(a+h) \)�� \( \displaystyle f'(a+h) \)�� \( \displaystyle A_1+ 2A_2h \)����A \( \displaystyle A_1+ 2A_2h \)����A
����ɇA�̗��ӂ�h�Ŕ��������
) \( \displaystyle f''(a+ h) \)�� \( \displaystyle f''(a+ h) \)�� \( \displaystyle 2A_2 \)����B \( \displaystyle 2A_2 \)����B
�@�A�B�̊e�X��h=0��������ƁC�萔 \( \displaystyle A_0,\hspace{2px}A_1,\hspace{2px}A_2 \)�̒l����܂�D \( \displaystyle A_0,\hspace{2px}A_1,\hspace{2px}A_2 \)�̒l����܂�D
) \( \displaystyle A_0=f(a) \) \( \displaystyle A_0=f(a) \)
) \( \displaystyle A_1=f'(a) \) \( \displaystyle A_1=f'(a) \)
}{2}) \( \displaystyle A_2=\frac{f''(a)}{2} \) \( \displaystyle A_2=\frac{f''(a)}{2} \)
����������
) \( \displaystyle f(a+ h) \)�� \( \displaystyle f(a+ h) \)��%2B f\apos(a)h%2B\frac{f\apos\apos(a)}{2}h^2) \( \displaystyle f(a)+ f'(a)h+\frac{f''(a)}{2}h^2 \) \( \displaystyle f(a)+ f'(a)h+\frac{f''(a)}{2}h^2 \)
(4)←
���ɁC(3)�ɂ�����a=0, h=x�Ƃ����Ƥ���_�̕t�߂ł̋ߎ�����������D
) \( \displaystyle f(x) \)�� \( \displaystyle f(x) \)��%2B f\apos(0)x%2B\frac{f\apos\apos(0)}{2}x^2) \( \displaystyle f(0)+ f'(0)x+\frac{f''(0)}{2}x^2 \) \( \displaystyle f(0)+ f'(0)x+\frac{f''(0)}{2}x^2 \)
|

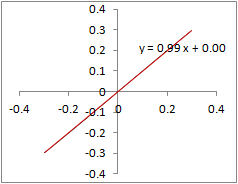
 �@Excel���g���āC1���ߎ����́u���������́v�_����������@
�@Excel���g���āC1���ߎ����́u���������́v�_����������@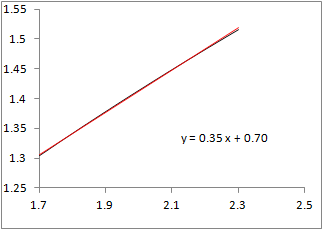
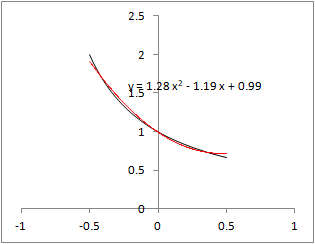
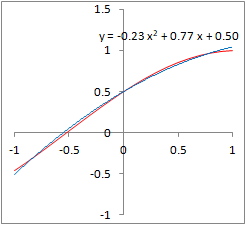
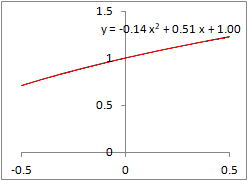 �@Excel���g���āC�Q���ߎ����́u���������́v�_����������@
�@Excel���g���āC�Q���ߎ����́u���������́v�_����������@