== 内分点の内分点 ==
■[解説]
△ABCにおいてA,B,Cの位置ベクトルを各々
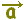 , ,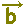 , ,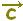 とするとき, とするとき,
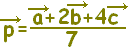
で表される点Pは,
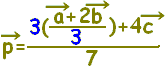
と変形することにより(割って掛ければ変わらない)
ABを2:1に内分する点D()を用いて,
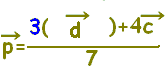
と表されます。
したがって,PはDCを4:3に内分する点となります。
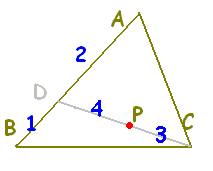
【要約】
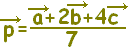
で表される点Pは,ABを2:1に内分する点をDとするとき,DCを4:3に内分する点。
この結果を使って,次のような三角形の面積比を答えさせる問題がよく見られます。
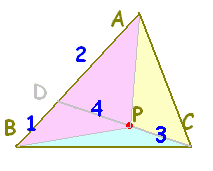
△ADP=4tとおくと、△ACP=3t
(高さが共通,底辺が4:3)
△BDP=2t(△ADPの半分)
△BCP=1.5t(△ACPの半分)
となるから
△ABP:△BCP:△CAPの面積比は,6t:1.5t:3t=12:3:6=4:1:2
(分子の係数の比:向かい側)
|
【一般に】
 \( \displaystyle \vec{p}=\frac{k\vec{a}+l\vec{b}+ m\vec{c}}{n} \) \( \displaystyle \vec{p}=\frac{k\vec{a}+l\vec{b}+ m\vec{c}}{n} \)
 \( (n=k+ l + m, \) \( (n=k+ l + m, \)
) \( k\gt 0,l\gt 0, m \gt 0) \) \( k\gt 0,l\gt 0, m \gt 0) \)
で表される点 ) \( P(\vec{p}) \) \( P(\vec{p}) \)は, ABを l:kに内分する点を Dとするとき, DCを m:(k+l)に内分する点となります。
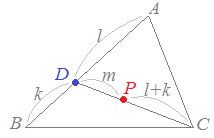
(解説)
まず,内分点の公式により,ABをl:kに内分する点Dの位置ベクトルを求めると
 \( \displaystyle \vec{d}=\frac{k\vec{a}+ l\vec{b}}{l+ k} \)…(1) \( \displaystyle \vec{d}=\frac{k\vec{a}+ l\vec{b}}{l+ k} \)…(1)
さらに,内分点の公式により,DCをm:(l+k)に内分する点Pの位置ベクトルを求めると
\vec{d}%2B m\vec{b}}{m %2B (l%2B k)}) \( \displaystyle \vec{p}=\frac{(l+ k)\vec{d}+ m\vec{b}}{m + (l+ k)} \)…(2) \( \displaystyle \vec{p}=\frac{(l+ k)\vec{d}+ m\vec{b}}{m + (l+ k)} \)…(2)
(1)を(2)に代入すると
(\frac{k\vec{a}%2B l\vec{b}}{l%2B k})%2B m\vec{b}}{m %2B (l%2B k)}&chco=0000ff) \( \displaystyle \vec{p}=\frac{(l+ k)(\dfrac{k\vec{a}+ l\vec{b}}{l+ k})+ m\vec{b}}{m + (l+ k)} \) \( \displaystyle \vec{p}=\frac{(l+ k)(\dfrac{k\vec{a}+ l\vec{b}}{l+ k})+ m\vec{b}}{m + (l+ k)} \)
 \( \displaystyle =\frac{ k\vec{a}+ l\vec{b}+ m\vec{c} }{k+ l+ m} \) \( \displaystyle =\frac{ k\vec{a}+ l\vec{b}+ m\vec{c} }{k+ l+ m} \)
(参考)
BCをm:lに内分する点をEとするとき,EAをk:(l+m)に内分する点と述べても同じです。
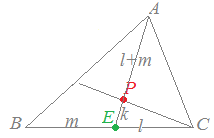
 \( \displaystyle \vec{e}=\frac{l\vec{b}+ m\vec{c}}{l+ m} \)…(3) \( \displaystyle \vec{e}=\frac{l\vec{b}+ m\vec{c}}{l+ m} \)…(3)
\vec{e}%2B k\vec{a}}{k %2B (l%2B m)}) \( \displaystyle \vec{p}=\frac{(l+ m)\vec{e}+ k\vec{a}}{k +(l+ m)} \)…(4) \( \displaystyle \vec{p}=\frac{(l+ m)\vec{e}+ k\vec{a}}{k +(l+ m)} \)…(4)
より
(\frac{l\vec{b}%2B m\vec{c}}{l%2B m})%2B k\vec{a}}{k %2B (l%2B m)}&chco=0000ff) \( \displaystyle \vec{p}=\frac{(l+ m)(\dfrac{l\vec{b}+ m\vec{c}}{l+ m})+ k\vec{a}}{k + (l+ m)} \) \( \displaystyle \vec{p}=\frac{(l+ m)(\dfrac{l\vec{b}+ m\vec{c}}{l+ m})+ k\vec{a}}{k + (l+ m)} \)
 \( \displaystyle =\frac{ k\vec{a}+ l\vec{b}+ m\vec{c} }{k+ l+ m} \) \( \displaystyle =\frac{ k\vec{a}+ l\vec{b}+ m\vec{c} }{k+ l+ m} \)
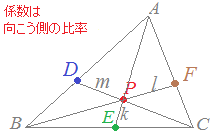
同様にして,
(\frac{k\vec{a}%2B m\vec{c}}{m%2B k})%2B l\vec{b}}{k %2B l%2B m}&chco=0000ff) \( \displaystyle \vec{p}=\frac{(m+ k)(\dfrac{k\vec{a}+ m\vec{c}}{m+ k})+ l\vec{b}}{k + l+ m} \) \( \displaystyle \vec{p}=\frac{(m+ k)(\dfrac{k\vec{a}+ m\vec{c}}{m+ k})+ l\vec{b}}{k + l+ m} \)
と変形すると,ACをm:kに内分する点をFとするとき,FBをl:(m+k)に内分する点を表しているとも言えます。
【ここが変形のポイント】

|
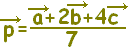
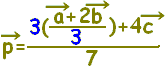
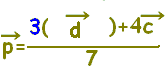

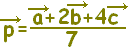






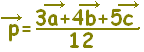 で表される点Pについて,次の空欄を埋めなさい。
で表される点Pについて,次の空欄を埋めなさい。