|
■ 三角関数の加法定理、積和の公式 ==センター試験2004年度・数II・B/第1問[2]の引用==(解答は筆者作成) |
[ヒント]
(1)
-180°<θ-a<θ≦180°,0°≦θ≦180° 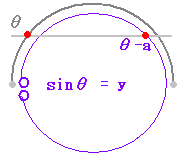 2θ=180°+a 別解 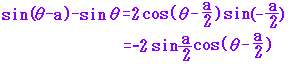
0°<a/2<90°,-90°<θ-a/2<180°だから θ-a/2=90° sin(θ-a)=1/2,sinθ=1/2,θ-a<θだから θ=150°,θ-a=30° よりa=120° |
| (2) |
[ヒント]
 |
|
■ 三角関数の加法定理、積和の公式 ==センター試験2004年度・数II・B/第1問[2]の引用==(解答は筆者作成) |
[ヒント]
(1)
-180°<θ-a<θ≦180°,0°≦θ≦180°  2θ=180°+a 別解 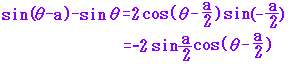
0°<a/2<90°,-90°<θ-a/2<180°だから θ-a/2=90° sin(θ-a)=1/2,sinθ=1/2,θ-a<θだから θ=150°,θ-a=30° よりa=120° |
| (2) |
[ヒント]
 |
| ●==メニューに戻る | |
|
=== 基本チェック === ■和→積の公式■ 加法定理により sin(α+β)=sinαcosβ+cosαsinβ・・・(1)(1)+(2) sin(α+β)+sin(α-β)=2sinαcosβ・・・(3) |
同様にして
(1)-(2) sin(α+β)-sin(α-β)=2cosαsinβ・・・(4) α+β=A,α-β=Bとおくと, |
|
■sinα=sinβ の解
0°<α,β<180°でsinα=sinβのとき, 図より α=180°-β 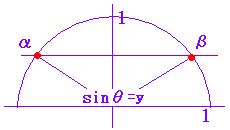 |
|
|
=== 基本確認テスト === 1 |
[ヒント]
0°<2θ<3θ<270°だから
3θ=180°-2θ 5θ=180° |
| 2 | [ヒント]
0°<θ<θ+50°<230°だから
θ+50°=180°-θ 2θ=130° |
| 3 | [ヒント]
和を積に直す公式により
 |
| ●==メニューに戻る | |