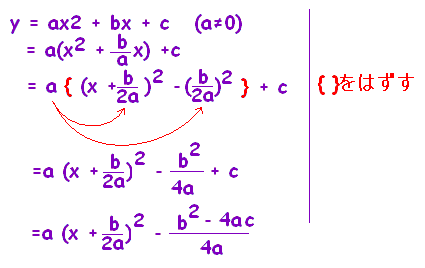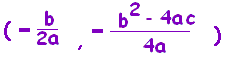[要約]
文字係数で書かれた2次関数の頂点の座標を求めるには、[1]公式を用いる方法 [2]公式を導く変形を身につける方法 の2つの方法が考えられますが、[2]の方法で行うことが多いようです。
([1]公式は覚えにくいからか?覚えなくても[2]の方法でできるので、覚える必要がないからか?)
[2]の方法で変形する際、次の例のように「係数を束ごと変形する技術」に慣れることが大切です。一部ずつ小出しにしていると計算がもつれてしまいます。
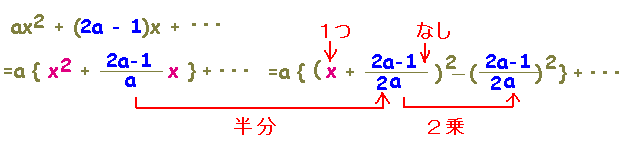
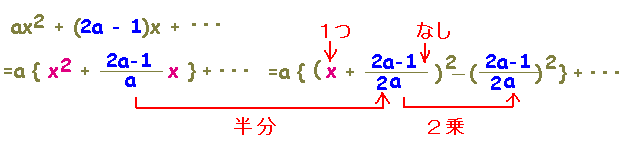
| ●文字係数の変形は「団体さん、お着き!」 |