== �ϕ��萔�̌��� ==
������F'(x)���^����ꂽ�ꍇ�C���̊�F(x)�͂����ϕ�������߂��܂����C���̏ꍇ�C�s��ϕ��Ƃ��Đϕ��萔C�����܂�Ȃ��`�ɂȂ�܂��D
���P��x�ɑ���F(x)�̒l
x=a�̂Ƃ�y=b�Ƃ����`�̎�
���Ȃ킿�CF(a)=b�Ƃ�����
���Ȃ킿�C�P�̒ʂ�_(a, b)
���^�����Ă���C���̐ϕ��萔C�͌��܂�܂��D
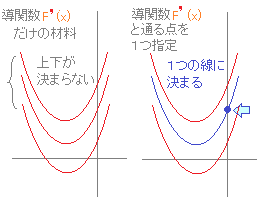 ������F(a)=b�̌`�̏��������u���������v�Ƃ����܂��D�i�����v�Ƃ������t�ɂ͂������K�v�͂Ȃ��C����x=0�̂Ƃ��̒l�����łȂ��C����x�̒l�ɑ���ꍇ�C�Ⴆ��F(3)=5�̂悤�ȏꍇ�ł��C���������ƌĂ�C���͊m�肵�܂��D�j
������F(a)=b�̌`�̏��������u���������v�Ƃ����܂��D�i�����v�Ƃ������t�ɂ͂������K�v�͂Ȃ��C����x=0�̂Ƃ��̒l�����łȂ��C����x�̒l�ɑ���ꍇ�C�Ⴆ��F(3)=5�̂悤�ȏꍇ�ł��C���������ƌĂ�C���͊m�肵�܂��D�j
�y�v�_�z
�@��ʂɁC����F'(x)�������^����ꂽ�Ƃ��C���̊�F(x)�̒萔��C�͌��܂�Ȃ��D
�@����F'(x)�Ə�������F(a)=b���^������ƁC�萔��C�����܂�C��F(x)���m�肷��
���m���̏��������� F(x)�͊m��ł��܂��n
=2x%2B 1,) \( F'(x)=2x+1,\hspace{5px}F(0)=1 \) \( F'(x)=2x+1,\hspace{5px}F(0)=1 \)…(1)
�~�m���̏��������� F(x)�͊m��ł��܂���n
=2x%2B 1,F\apos (0)=1&chco=ff0000) \( F'(x)=2x+1,\hspace{5px}F'(0)=1 \) \( F'(x)=2x+1,\hspace{5px}F'(0)=1 \)…(2)
(1)�ł́C =x^2 %2B x %2B C) \( F(x)=x^2 +x+C \) \( F(x)=x^2 +x+C \)�Ə������� F(0)=1���� C�����߂��܂���
(2)�ł� =x^2 %2B x %2B C) \( F(x)=x^2 +x+C \) \( F(x)=x^2 +x+C \)�ɑ��āC F'(0)=1�͏��������ɂȂ��Ă��炸�C C�����߂��|���肪����܂���D�i F'(x)�̎����肾�ƁC�P�� C���܂܂�Ă��Ȃ��̂ŁC C�����߂邱�Ƃ��ł��܂���j
�s���t
F'(x)=2x, F(1)=3�̂Ƃ��CF(x)�����߂Ȃ���.
�i���āj
F'(x)=2x������\( \displaystyle F(x)=\int 2xdx=x^2+C \)
F(1)=3������1+C=3→C=2
�䂦��\( F(x)=x^2+2\)�E�E�E(��)
�s�v�_�t
�܂��s��ϕ������߁C���ɂb���߂܂�.
|
 �������E�L�����E�������̕s��ϕ�
�������E�L�����E�������̕s��ϕ�
 ������(�L����)�̕s��ϕ�
������(�L����)�̕s��ϕ�
 ��(2)
��(2)
 ��(3)
��(3)
 ��(4)
��(4)
 ��(�܂Ƃ�)
��(�܂Ƃ�) �s��ϕ��̒u���ϕ�
�s��ϕ��̒u���ϕ�
 ��(2)
��(2)
 �s��ϕ��̕����ϕ�
�s��ϕ��̕����ϕ�
 ��(2)
��(2)
 �w�����E�ΐ����̕s��ϕ�
�w�����E�ΐ����̕s��ϕ�
 ��(2)
��(2)
 �O�p���̕s��ϕ�
�O�p���̕s��ϕ�
 ��(2)
��(2)
 �s��ϕ��i�܂Ƃ�1�j
�s��ϕ��i�܂Ƃ�1�j
 ��(2)
��(2)
 �s��ϕ��̑Q����
�s��ϕ��̑Q����
 log x�̕s��ϕ�
log x�̕s��ϕ�
 sin x�̕s��ϕ�
sin x�̕s��ϕ� cos x�̕s��ϕ�
cos x�̕s��ϕ�
 sin x,cos x�̕s��ϕ�
sin x,cos x�̕s��ϕ� tan x,cot x�̕s��ϕ�
tan x,cot x�̕s��ϕ�

