数学Ⅰ.実数と根号（公式と例）

...(ＰＣ版)メニューに戻る
*** 科目 ***
数Ⅰ・Ａ数Ⅱ・Ｂ数Ⅲ 高卒・大学初年度
*** 単元 ***
数と式不等式二次関数二次不等式三角比三角比と図形集合・命題・証明順列・組合せ確率整数の性質

※高校数学Ⅰ・Ａの「数と式」について，このサイトには次の教材があります．
この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください．　が現在地です．

↓単項式と多項式
↓指数法則
↓展開公式1
↓展開公式2
↓置き換えによる展開
↓展開の順序
↓展開公式の応用問題
↓対称式の値
↓２次式の因数分解
↓いろいろな因数分解
↓１文字について整理
↓たすき掛け因数分解
↓同(1文字)
↓同(1文字)2
↓たすき掛け因数分解(2文字)
↓同(2文字)2
↓３次以上の因数分解
↓因数分解の応用問題
↓因数分解の入試問題
↓実数と根号（公式と例）
↓根号計算
↓同2
↓分母の有理化
↓無理数の独立
↓式の値(無理数の対称式)
↓xⁿ+1/xⁿの値
↓センター問題平方根の計算
↓根号計算の入試問題
↓二重根号
↓文字式を含む根号計算
↓絶対値
↓絶対値2つの外し方
↓絶対値の入試問題
センター共通数と式(2013～)

== 数学Ⅰ.実数と根号（公式と例） ==

　このページは，教科書に太枠で書かれているレベルの公式を一覧表にして，各々の使い方を２題ずつ示したものです．
　高校の定期試験や大学入試問題などと比較すると，内容的に「非常に薄い」ものですので，その点よろしく．
　これらの公式を始めてみる人が，このページだけで身に着けるのは無理です．一度学習した人が，思い出す場合を想定しています．
　もう少し詳しい内容，証明などがあるページはリンクで示しています．

【1. 実数の分類】

【整数の例】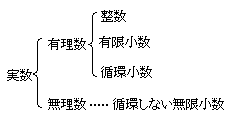

正の整数1, 2, 3, 4, ...
0
負の整数−1, −2, −3, −4, ...

【有限小数の例】

0.7, 1.5, 2.13, 3.456, ...
−0.3, −1.2, −2.04, −13.124,...

【循環小数の例】

\frac{1}{3} = 0.33 \dots = 0. \dot{3}

1.4545 \dots = 1. \dot{4} \dot{5}

2.34567567 \dots = 2.34 \dot{5} 6 \dot{7}

【無理数の例】

根号

\sqrt{2} = 1.41421356 \dots

円周率

π = 3.141592 \dots

自然対数の底

e = 2.71828 \dots

※間違いやすいこと(1)
　有理数と無理数の違いは，有限小数と無限小数の違いではない．すなわち，「有限小数＝有理数，無限小数＝無理数」と考えていたら，それは間違いです．
　有限小数または循環小数（循環する無限小数）が有理数です．上の例のうち，

0.33 \dots = 0. \dot{3}

は循環する無限小数で有理数です．
　これに対して，循環しない無限小数が無理数です．はっきり言えば，「無限」が相違点ではなく「循環する，循環しない」の違いが有理数と無理数の違いです．

	有理数	無理数
分数との関係	整数整数で表せる◎	整数整数で表せない
小数との関係	循環する無限小数（有限小数を含む）	循環しない無限小数

　上の表は◎の部分を切口として読むと分かり易いです．

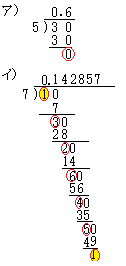　すなわち，有理数を

整数

で表せるもの

と定義します．
　これを小数に直すときに，「商」ではなく「余り」の方に着目することが重要です．
　正の整数nで割ったときの余りrは0≦r≦n−1のn種類ありますが，
ア）

\frac{3}{5} = 0.6

のように計算の途中で，余り０が登場したら，割り切れて有限小数になります．
イ）

\frac{1}{7} = 0.142857 \dots

のように，どこまで行っても割り切れない場合，右図の

◯

で示した余りは，０以外７以外の数字1,2,3,4,5,6の６通りあり，

◯

で示したように同じ余りが再登場すると，そこから先は同じ割り算の繰り返しになります．したがって，分母がnの分数は，最も長くても循環節の長さがn−1の循環小数になります．
　結局，

整数

で表される有理数は，有限小数になるか循環小数になるかのいずれかです．そうでないものが無理数です．

　実は，０以外の整数や有限小数はすべて循環する無限小数で表すことができます.

1 = 0.999 \dots

2 = 1.999 \dots

3.4 = 3.3999 \dots

- 12.25 = - 12.24999 \dots

このようにして，０以外のすべての「有理数」は「循環する無限小数」で，「無理数」は「循環しない無限小数」であるとも言えます．
　（整数）÷（整数）で与えられる分数の値はすべて有理数ですが，それが有限小数になるのは分母が2と5の倍数だけからできている場合です．それ以外の素因数（3, 7, 11など）が分母に含まれる分数は，循環する無限小数になります．こうした事情は10進法で表しているためで，例えば10進法の

\frac{1}{3}

は3進法で表せば有限小数になり，

\frac{1}{2}

は3進法で表せば無限小数になります．

高校1年生には，難し過ぎて分からん！

高校3年間で
他に言える場所がないので
ここに書いています

※間違いやすいこと(2)
　根号で表されるものだけが無理数である訳ではありません．循環しない無限小数であれば無理数なので，次のような小数も無理数です．

0.101001000100001 \dots

1.011011101111011111 \dots

　円周率や自然対数の底は，次のような数列の和（級数）で表されます．

π = 4 {1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} \dots}

e = 1 + \frac{1}{1} + \frac{1}{1 \cdot 2} + \frac{1}{1 \cdot 2 \cdot 3} + \frac{1}{1 \cdot 2 \cdot 3 \cdot 4} \dots

	代数的無理数	超越数
	整数や有理数を係数とするｎ次方程式の解となる無理数	整数や有理数を係数とするｎ次方程式の解として書けない無理数
例	$\sqrt{2} = 1.4142 \dots$ $\sqrt{3} = 1.7320 \dots$ $\sqrt[3]{2} = 1.25992 \dots$	$π = 4 {1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} \dots}$ $e = 1 + \frac{1}{1} + \frac{1}{1 \cdot 2} + \frac{1}{1 \cdot 2 \cdot 3} + \dots$ $\log_{e} 2 = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} \dots$

【2. 根号計算】

\sqrt{a^{2}} = | a |

…(2.1)
a> 0, b>0のとき

\sqrt{a} \sqrt{b} = \sqrt{a b}

…(2.2)

\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}

…(2.3)

a > 0, k > 0

のとき

\sqrt{k^{2} a} = k \sqrt{a}

…(2.4)

もっと詳しい教材はこちら

【例2.1】

\sqrt{3^{2}} = \sqrt{9} = 3

\sqrt{(- 3)^{2}} = \sqrt{9} = 3 \leftarrow {- (- 3)}

※a<0のとき

\sqrt{a^{2}} = a

ではないことに注意

【例2.2】

\sqrt{2} \sqrt{3} = \sqrt{6}

\sqrt{3} \sqrt{5} = \sqrt{15}

【例2.3】

\frac{\sqrt{6}}{\sqrt{2}} = \sqrt{\frac{6}{2}} = \sqrt{3}

\frac{\sqrt{27}}{\sqrt{3}} = \sqrt{\frac{27}{3}} = \sqrt{9} = 3

【例2.4】

\sqrt{12} = \sqrt{2^{2} \times 3} = 2 \sqrt{3}

\sqrt{18} = \sqrt{2 \times 3^{2}} = 3 \sqrt{2}

分母の有理化
a>0, b>0のとき

\frac{1}{\sqrt{a}} = \frac{\sqrt{a}}{a}

…(2.5)

\frac{1}{\sqrt{a} + \sqrt{b}} = \frac{\sqrt{a} - \sqrt{b}}{a - b}

…(2.6)

\frac{1}{\sqrt{a} - \sqrt{b}} = \frac{\sqrt{a} + \sqrt{b}}{a - b}

…(2.7)

もっと詳しい教材はこちら

【例2.5】

\frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}

\frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}

【例2.6】

\frac{1}{\sqrt{5} + \sqrt{3}} = \frac{\sqrt{5} - \sqrt{3}}{5 - 3} = \frac{\sqrt{5} - \sqrt{3}}{2}

\frac{1}{\sqrt{2}} = \frac{\sqrt{2} - 1}{2 - 1} = \sqrt{2} - 1

【例2.7】

\frac{1}{\sqrt{2} - \sqrt{3}} = \frac{\sqrt{2}}{2 - 3} = - \sqrt{2} - \sqrt{3}

\frac{1}{2 - \sqrt{3}} = \frac{2 + \sqrt{3}}{4 - 3} = 2 + \sqrt{3}

二重根号
a>0, b>0のとき

\sqrt{a + b + 2 \sqrt{a b}} = \sqrt{a} + \sqrt{b}

…(2.8)
a>b>0のとき

\sqrt{a + b - 2 \sqrt{a b}} = \sqrt{a} - \sqrt{b}

…(2.9)

もっと詳しい教材はこちら

【例2.8】

\sqrt{5 + 2 \sqrt{6}} = \sqrt{2} + \sqrt{3}

\sqrt{7 + 2 \sqrt{12}} = \sqrt{4} + \sqrt{3} = 2 + \sqrt{3}

【例2.9】

\sqrt{8 - 2 \sqrt{15}} = \sqrt{5} - \sqrt{3}

\sqrt{9 - 2 \sqrt{20}} = \sqrt{5} - \sqrt{4} = \sqrt{5} - 2

■このサイト内のGoogle検索■

△このページの先頭に戻る△【アンケート送信】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．

○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）

質問に対する回答の中学版はこの頁，高校版はこの頁にあります