線分ABをm:nに外分する点Qとは,AQ:QB=m:n
となるような点QをABの外側にとったもの。(右図参照)
Aの外側にあればm<nとなり、Bの外側にあれば
m>nとなる。(この項目の復習はこちら)

1
2点A,Bを結ぶ線分ABをm:nに外分する点Qの位置ベクトルは
2
△ABCの頂点A,B,Cの位置ベクトルを各々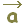 ,
,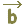 ,
,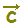 とするとき,△ABCの重心Gの位置ベクトルは
とするとき,△ABCの重心Gの位置ベクトルは
△ABCの頂点A,B,Cの位置ベクトルを各々
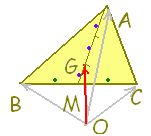
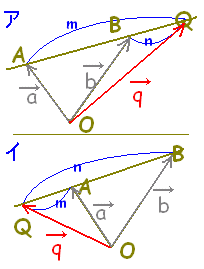
■外分点の位置ベクトル、重心の位置ベクトル
|
 |
|
■[要点] 1 2点A,Bを結ぶ線分ABをm:nに外分する点Qの位置ベクトルは 2
△ABCの頂点A,B,Cの位置ベクトルを各々  |
 |
|
■[解説] 1 m>n のとき,図アにより
|
m<n のとき,図イにより AQ:QB=m:n だからAQ:AB=m:(n-m) AQ,ABは逆向きだから 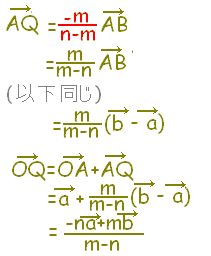 |
| 2 BCの中点Mの位置ベクトルは 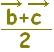 次に,A(
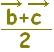 ) を2:1に内分する点がGだから, ) を2:1に内分する点がGだから,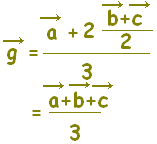 |
三角形の重心は,元々は各頂点から対辺に引いた中線が交わる点として定義さ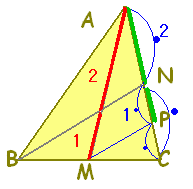 れるが,「中線の交点を求める」ためには,直線のベクトル方程式を学ぶ必要がある。 れるが,「中線の交点を求める」ためには,直線のベクトル方程式を学ぶ必要がある。ここでは、三角形の重心の定義ではなく,定義から導かれる一つの性質:「重心は頂点と対辺を2:1に内分する」を用いて,重心を求める。 MからBNに平行線を引き,ACとの交点をPとすると, PN:NA=1:2だから, AG:GM=2:1 |
|
■[問題] △ABCの頂点の位置ベクトルを (初めに問題を選び、次に選択肢を選びなさい。合っていれば消えます。なお、選択肢にはジョーカが含まれています。暗算は難しいので計算用紙を使いましょう。)
|
|||
|
解説 |
|||