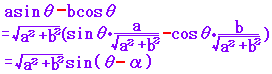■三角関数の合成公式
◆難易：教科書程度◆--難しいと思う人は下の基本チェックを先に↓
◆センター試験2002年度数II・Ｂ第１問［１］の引用◆
ａを正の定数とし，角θの関数
f(θ)=sin(ａθ)+√3cos(ａθ)
を考える。
(1)　f(θ)=［ア］sin(ａθ+［イウ］°)である。
［ア］=，［イウ］=
(2)　f(θ)=0を満たす正の角θのうち
　最小のものは
　であり，小さい方から数えて４番目と５番目のものは，それぞれ
，
　である。
［エオカ］=，［キクケ］=，［コサシ］=
　　
(3)　0°≦θ≦180°の範囲で，f(θ)=0を満たすθがちょうど4個存在するようなａの範囲は
である。
［スセ］=，［ソ］=，［タチ］=，［ツ］=

［ヒント］ ［ヒント］ ［ヒント］
■基本のチェック
■三角関数の合成公式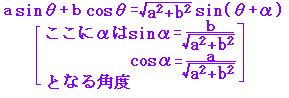
◆解説1◆加法定理から計算によって示す方法
sinθcosα+cosθsinα=sin(θ+α)・・・(4)だから
　例えば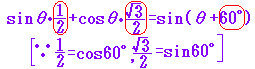
と合成できる

　しかし，一般にはａ，ｂがそのままの値でcosα，sinαになっているとは限らないので，何倍か掛けたり割ったりして一つの角度αのcosα，sinαになるように変形する。
　例えば

「一般の場合
　　
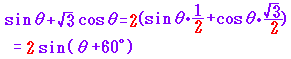ａやｂが負の値のときはαを第２，３，４象限の角とします。
」

◆解説2◆図で示す方法
［注意］
■積→和の公式は、sinＡ±sinＢ，cosＡ±cosＢのように同種の三角関数の和差です。
■合成公式は、係数は付きますが１つの角度についての　ａsinθ+ｂcosθの形です。

■sinＡ±cosＢ　<===　異なる種類の三角関数で角度も異なるもの
　ａ･sinθ+ｂ･sinθ　<===　同種の三角関数だが係数が異なるもの
　ａ･sinC+ｂ･cosＤ　<===　異なる種類の三角関数で、係数も異なり、角度も異なるもの
==>　これらはについては、積→和の公式、合成公式のいずれでも扱っていません。
■基本のチェックテスト
１　三角関数の合成公式
(1) ｓｉnθ+cosθ=ｓｉｎ(θ+[イ]°)　
(0°＜［イ］＜180°)
［ア］=，［イ］=
(2) √3sinθ-cosθ=［ウ］sin(θ-[エ]°)
(0°＜［エ］＜180°)
［ウ］=，［エ］=
(3) 2sinθ+cosθ=sin(θ+α)
(ここで，αは　
となる角)
［オ］=，［カ］=，［キ］=

［ク］=，［ケ］=

 ［ヒント］ ［ヒント］ ［ヒント］
■基本のチェック
■ｙ=sin ｋθ のグラフ
y=sin2θのグラフはy=sinθのグラフを横方向に半分に縮めたものです。
y=sin3θのグラフはy=sinθのグラフを横方向に３分の1に縮めたものです。
(ｘ軸方向に伸びるのでなく縮みます<==角度が速く回るから。)
θ
0
15
30
45
60
75
90
105
120
135
150
165
180
2θ
0
30
60
90
120
150
180
210
240
270
300
330
360
3θ
0
45
90
135
180
225
270
315
360
405
450
495
540
0°＜θ＜180°において
y=sinθとｘ軸の共有点はありません。
y=sin2θとｘ軸の共有点は１つあります。
y=sin3θとｘ軸の共有点は2つあります。

y=sinｋ（θ-30°）のグラフは，y=sinｋθのグラフをｘ軸の正の向きに30°だけ平行移動したものなので
0°＜θ＜180°において
y=sin(θ-30°)とｘ軸の共有点は１つあります。
y=sin2(θ-30°)とｘ軸の共有点は2つあります。
y=sin3(θ-30°)とｘ軸の共有点は3つあります。

ｋ＞0のとき，0°＜θ＜180°において
y=sinkθのグラフがｘ軸と1つの共有点を持つような定数ｋの値の範囲は1＜ｋ≦2
y=sinkθのグラフがｘ軸と2つの共有点を持つような定数ｋの値の範囲は2＜ｋ≦3
y=sinkθのグラフがｘ軸と3つの共有点を持つような定数ｋの値の範囲は3＜ｋ≦4

●===メニューに戻る