== �����a�̑�����, �ڎ� ==���u���[�}�O�v�^�̓��P�����i�t�B�{�i�b�`�̓��P�����j
\((a^2+b^2)(x^2+y^2)=(ax-by)^2+(ay+bx)^2\)…(1.1)
�܂��� \((a^2+b^2)(x^2+y^2)=(ax+by)^2+(ay-bx)^2\)…(1.2)
�Z�����a�̐�����ς̉��Z�ɂ��ĕ��Ă���
�����a�R�g�̐� \((a^2+b^2)(x^2+y^2)(p^2+q^2)\) \(=\{(ax-by)p-(ay+bx)q\}^2\) \(+\{(ax-by)q-(ay+bx)p\}^2\)…(1.4) �����a�S�g�̐� \((a^2+b^2)(x^2+y^2)(p^2+q^2)(s^2+t^2)\) \(=\Big\lbrack\big\{(ax-by)p-(ay+bx)q\big\}s\) \(-\big\{(ax-by)q+(ay+bx)p\big\}t\Big\rbrack^2\) \(+\Big\lbrack\big\{(ax-by)p-(ay+bx)q\big\}t\) \(+\big\{(ax-by)q+(ay+bx)p\big\}s\Big\rbrack^2\) …(1.5) ���I�C���[�̎l�����P���� |
�Z���O�����W���̎l�������藝�S�Ă̎��R�������X�i�����Ƃ��j�l�̕������̘a�ŕ\�����…(2.3)�Z���R�r�̎l�����藝���R�������X�l�̕������̘a�ŕ\�����@�̐�…(2.4) |
|
�u�����̕������̘a����Ȃ�W���v���C�ς̉��Z�ɂ��ĕ��Ă������Ƃ̏ؖ��F �@�����S�̂̏W����\(Z\)�ŕ\���Ƃ��C�����̕������̘a����Ȃ�W����\(A\)�Ƃ���
\(A=\{a^2+b^2\hspace{5px}|\hspace{5px}a,b\in Z\}\)�Ƃ����
�i��j\(x,y\in A\Longrightarrow xy\in A\) \(x,y\in A\) �Ȃ�� \(x=a^2+b^2,y=c^2+d^2\)�ƂȂ鐮�� \(a,b,c,d\) �����݂��邩��C �@\(xy=(a^2+b^2)(c^2+d^2)=(ac-bd)^2+(ad+bc)^2\)�Ə����邱�ƂɂȂ�C\(xy\in A\) ��������D �����a�R�g�̐� (1.4) �̏ؖ�←
���ȉ��̂悤�ȕό`��ڂŒǂ��Ă����̂́C���\�ȋ�ɂ��D�i�ԈႢ�̓_������ρI�I�j
(1.1) �@�X���X���Ƃł���X�g�C�b�N�ȕ��͕ʂƂ��āC�������}�l�́C�����Ɗy�����V�т̗v�f������� �u��`���Ă��s�v�c�ȓ싞�ʂ�����C���ڂɂƂ܂�Ό��ւƕԂ��`♫���C�V���v�Ȃǂƍ����̎������̂��R�c����
\((a^2+b^2)(x^2+y^2)\)
�ɂ����āC\(=(ax-by)^2+(ay+bx)^2\) \(A=ax-by\) \(B=ay+bx\) �Ƃ����� \((a^2+b^2)(x^2+y^2)\) \(=\textcolor{red}{A}^2+\textcolor{blue}{B}^2\) �����ŁC�����a�R�g�̐ς��l����� \((a^2+b^2)(x^2+y^2)(p^2+q^2)\) \(=(\textcolor{red}{A}^2+\textcolor{blue}{B}^2)(p^2+q^2)\)
��`���ڂɂƂ܂�Ό��ւƕԂ��`♫
(1.1)�ɂ��\(=(\textcolor{red}{A}p-\textcolor{blue}{B}q)^2+(\textcolor{red}{A}q+\textcolor{blue}{B}p)^2\) \(=\Big\{\textcolor{red}{(ax-by)}p-\textcolor{blue}{(ay+bx)}q\Big\}^2+\Big\{\textcolor{red}{(ax-by)}q+\textcolor{blue}{(ay+bx)}p\Big\}^2\) �͂Q���̕����̘a�ɂȂ��Ă���D_�� �����a�S�g�̐� (1.5) �̏ؖ�← (1.4)�ɂ�� \((a^2+b^2)(x^2+y^2)(p^2+q^2)\) \(=\Big\{(ax-by)p-(ay+bx)q\Big\}^2+\Big\{(ax-by)q+(ay+bx)p\Big\}^2\) �ɂ����āC \(C=(ax-by)p-(ay+bx)q\) \(D=(ax-by)q+(ay+bx)p\) �Ƃ����� \((a^2+b^2)(x^2+y^2)(p^2+q^2)=\textcolor{red}{C}^2+\textcolor{blue}{D}^2\) �����ŁC�����a�S�g�̐ς��l����� \((a^2+b^2)(x^2+y^2)(p^2+q^2)(s^2+t^2)\) \(=(\textcolor{red}{C}^2+\textcolor{blue}{D}^2)(s^2+t^2)\)
��`���ڂɂƂ܂�Ό��ւƕԂ��`♫
(1.1)�ɂ��\(=(\textcolor{red}{C}s-\textcolor{blue}{D}t)^2+(\textcolor{red}{C}t+\textcolor{blue}{D}s)^2\) \(=\Big\lbrack\big\{\textcolor{red}{(ax-by)p-(ay+bx)q}\big\}s-\big\{\textcolor{blue}{(ax-by)q+(ay+bx)p}\big\}t\Big\rbrack^2\) \(+\Big\lbrack\big\{\textcolor{red}{(ax-by)p-(ay+bx)q}\big\}t+\big\{\textcolor{blue}{(ax-by)q+(ay+bx)p}\big\}s\Big\rbrack^2\) �͂Q���̕����̘a�ɂȂ��Ă���D_�� ���ȏ�̂悤�ɂ���C�A�[�I�ɕ����a���g�̐ςł��Q���̕����̘a�ɂȂ邱�Ƃ�������D |
���I�C���[�̎l�����P���� (2.1)�̏ؖ�←
\((a^2+b^2+c^2+d^2)(x^2+y^2+z^2+w^2)\)
���ؖ�����ɂ́C���ӂ����ꂼ��W�J���Ĕ�r����悢���C���̂悤�Ɍ����ƁC���e�ɂ��Ė��������ŁC��ʌv�Z�̍�������������邱�ƂɂȂ�D\(=(ax+by+cz+dw)^2\) \(+(ay-bx+cw-dz)^2\)
\(+(az-bw-cx+dy)^2\)
\(+(aw+bz-cy-dx)^2\)…(2.1)
�@�����ł́C�u���[�}�O�v�^�̓��P����(1.2)��ό`���ăI�C���[�̎l�����P���� (2.1)���ؖ����Ă݂�D
�@��Ŏ����悤�ɁC�Ɨ���4�����~2�̎����當���������炵�ēƗ���2�����~2�̎�����邱�Ƃ͊ȒP�ł��邪�C�Ɨ���2�����~2�̎���ό`���ēƗ���4�����~2�̎�����邱�Ƃ͓�Փx�������D�i�g���ɂȂ�j
�@�E�ӂ�W�J���邱�Ƃ���n�߂�D�@�l�b�g�Œ��ׂĂ��C���̕ό`�͌�����Ȃ������̂ŁC���܂��s���Ζ��Ƃ������ƂŁC���������ҁI�I �i�E�Ӂj=
\((ax+by)^2\)
\(+(ay-bx)^2\)
\(+(cz+dw)^2\)
\(+(cw-dz)^2\)
\(+2abxy+2cdzw\)
\(-2abxy-2cdzw\)
\((az-bw)^2\)
\(+(aw+bz)^2\)
\(+(cx-dy)^2\)
\(+(cy+dx)^2\)
\(-2abzw-2cdxy\)
\(+2abzw+2cdxy\) �@�D�F�̔j���ň͂܂ꂽ�����͏�����D�ԁC�C�C���̔j���ň͂܂ꂽ�����́C���ꂼ��(1.2)�̎� �@\((a^2+b^2)(x^2+y^2)=(ax+by)^2+(ay-bx)^2\)…(1.2) ���E���獶�ɓǂނ�
\((a^2+b^2)(x^2+y^2)\)
\((c^2+d^2)(z^2+w^2)\)
\((a^2+b^2)(z^2+w^2)\)
\((c^2+d^2)(x^2+y^2)\)
�ƂȂ邩�� �i�E�Ӂj=\((a^2+b^2)(x^2+y^2+z^2+w^2)\) \(+(c^2+d^2)(x^2+y^2+z^2+w^2)\) \(=(a^2+b^2+c^2+d^2)(x^2+y^2+z^2+w^2)\) _�� |
|
���I�C���[�̎l�����P���� (2.2)�̏ؖ�← �I�C���[�̎l�����P�����́C�����̏ꍇ(2.1)�̌`�ŏ�����邪�C����(2.2)�̌`�ɂ��Ă����ƁC�g���₷�����Ƃ�����D (2.1)�̎��ɂ����āC\(x\)�̑����\(-x\)��������� \((a^2+b^2+c^2+d^2)(x^2+y^2+z^2+w^2)\) \(=(-ax+by+cz+dw)^2\) \(+(ay+bx+cw-dz)^2\)
\(+(az-bw+cx+dy)^2\)
\(+(aw+bz-cy+dx)^2\)
\(=(ax-by-cz-dw)^2\)\(+(ay+bx+cw-dz)^2\)
\(+(az-bw+cx+dy)^2\)
\(+(aw+bz-cy+dx)^2\)…(2.2)
�I�C���[�̎l�����P����(2.1),(2.2)�̑��̃o���G�[�V�����̍����@���₷���i�ԈႢ�ɂ����j���邽�߂ɁC\(a,b,c,d\)�͓����c��ɑ����āC�������ؖ��ł��Ă���(2.1)����X�^�[�g���āC\(b,c,d\)����1�C2�C(3��)�̕�����ς��Ă����D�������C3�ς��邱�Ƃ͎c��1������ς��邱�ƂƓ���������C\(a\)�����͐��̕����ɌŒ肵�Ă����D ����ɁC\(x,y,z,w\)����1�C2�C3�C4�̕�����ς������̂��S�Đ��藧�D \((a^2+b^2+c^2+d^2)(x^2+y^2+z^2+w^2)\)
\(=(ax+by+cz+dw)^2\)
\(+(ay-bx+cw-dz)^2\) \(+(az-bw-cx+dy)^2\) \(+(aw+bz-cy-dx)^2\)
\(=(ax-by+cz+dw)^2\)
\(+(ay+bx+cw-dz)^2\) \(+(az+bw-cx+dy)^2\) \(+(aw+bz-cy-dx)^2\)
\(=(ax+by+cz+dw)^2\)
\(+(ay-bx-cw-dz)^2\) \(+(az-bw+cx+dy)^2\) \(+(aw+bz+cy-dx)^2\) �Ȃ� ���I�C���[�̎l�����P����(2.2)����u���[�}�O�v�^�̓��P����(1.1)���ؖ�← (2.2)�̗��ӂ�\(c=d=z=w=0\)��������� \((a^2+b^2)(x^2+y^2)\) \(=(ax-by)^2+(ay+bx)^2\)…(1.1)�@_�� �Ȃ��C���I�C���[�̎l�����P����(2.1)����\(d=w=0\)��������3�����~2�̎�������Ă��C�O�����P�����ɂ͂Ȃ�Ȃ��F�E�ӂ͎l�����̎��ɂȂ�D \((a^2+b^2+c^2)(x^2+y^2+z^2)\) \(=(ax+by+cz)^2\) \(+(ay-bx)^2\)
\(+(az-cx)^2\)
\(+(bz-cy)^2\)
�@���̎��́C�R�[�V�[�E�V�������c�̕s�����̏ؖ��@\((a^2+b^2+c^2)(x^2+y^2+z^2)\geqq (ax+by+cz)^2\) �ƂȂ��Ă���C����������������� �@\(a:b:c=x:y:z\Longleftrightarrow \vec{u}=(a,b,c)/\!/\vec{v}=(x,y,z)\) ��������Ă���D |
�Z���O�����W���̎l�������藝����u�S�Ă̎��R�������X�i�����Ƃ��j�l�̕������̘a�ŕ\�����v���C��̗�Ŏ����F �i�����X�l�Ƃ́C���傤�ǎl�Ƃ͈Ⴂ�C�P�`�S�܂łƂ������Ɓj
\(1=1^2\) ←1��
\(2=1^2+1^2\) ←2�� \(3=1^2+1^2+1^2\) ←3�� \(4=1^2+1^2+1^2+1^2\) ←4�� �܂��� \(4=2^2\) ←1�� \(5=1^2+2^2\) ←2��
\(6=1^2+1^2+2^2\) ←3��
\(7=1^2+1^2+1^2+2^2\) ←4�� \(8=2^2+2^2\) ←2�� \(9=1^2+2^2+2^2\) ←3�� �܂��� \(9=3^2\) ←1�� \(10=1^2+1^2+2^2+2^2\) ←4�� �܂��� \(10=1^2+3^2\) ←2�� �@���O�����W���̎l�������藝�́C�I�C���[�̎l�����P�������g���ďؖ������D �Z���R�r�̎l�����藝����u���R�������X�l�̕������̘a�ŕ\�����@�̐��v����̓I�Ȍv�Z�Ŏ����D ���R�� \(N\) �ɑ��āC4�̕������̘a�ŕ\�����@�̐��� \(r_4(N)\) �ŕ\���� \(\displaystyle r_4(N)=8\sum_{d|N,4\nmid d}d\)
�����ŁC���a�L�����́u4�Ŋ����Ȃ�\(N\)�̖�\(d\)�i1��N���܂ށj��S�������v���Ƃ�\���D�s��t�@\(r_4(6)=8(1+2+3+6)=96\) �� 6��4�̕������̘a�ŕ\�����@�́C�u�������C���ו����S���������Ɓv96�ʂ�
\(0^2+(\pm 1)^2+(\pm 1)^2+(\pm 2)^2\) →8�ʂ�
����Ȃ��̂܂ŁC��ʂ��Đ�����̂��`�I\(0^2+(\pm 1)^2+(\pm 2)^2+(\pm 1)^2\) →8�ʂ� \(0^2+(\pm 2)^2+(\pm 1)^2+(\pm 1)^2\) →8�ʂ� \((\pm 1)^2+0^2+(\pm 1)^2+(\pm 2)^2\) →8�ʂ� \((\pm 1)^2+0^2+(\pm 2)^2+(\pm 1)^2\) →8�ʂ� \((\pm 2)^2+0^2+(\pm 1)^2+(\pm 1)^2\) →8�ʂ� \((\pm 1)^2+(\pm 1)^2+0^2+(\pm 2)^2\) →8�ʂ� \((\pm 1)^2+(\pm 2)^2+0^2+(\pm 1)^2\) →8�ʂ� \((\pm 2)^2+(\pm 1)^2+0^2+(\pm 1)^2\) →8�ʂ� \((\pm 1)^2+(\pm 1)^2+(\pm 2)^2+0^2\) →8�ʂ� \((\pm 1)^2+(\pm 2)^2+(\pm 1)^2+0^2\) →8�ʂ� \((\pm 2)^2+(\pm 1)^2+(\pm 1)^2+0^2\) →8�ʂ� �s��t�@\(r_4(9)=8(1+3+9)=104\) �� 9��4�̕������̘a�ŕ\�����@�́C�u�������C���ו����S���������Ɓv104�ʂ�
\(0^2+(\pm 1)^2+(\pm 2)^2+(\pm 2)^2\) →8�ʂ�
\(0^2+(\pm 2)^2+(\pm 1)^2+(\pm 2)^2\) →8�ʂ� \(0^2+(\pm 2)^2+(\pm 2)^2+(\pm 1)^2\) →8�ʂ� \((\pm 1)^2+0^2+(\pm 2)^2+(\pm 2)^2\) →8�ʂ� \((\pm 2)^2+0^2+(\pm 1)^2+(\pm 2)^2\) →8�ʂ� \((\pm 2)^2+0^2+(\pm 2)^2+(\pm 1)^2\) →8�ʂ� \((\pm 1)^2+(\pm 2)^2+0^2+(\pm 2)^2\) →8�ʂ� \((\pm 2)^2+(\pm 2)^2+0^2+(\pm 2)^2\) →8�ʂ� \((\pm 2)^2+(\pm 2)^2+0^2+(\pm 1)^2\) →8�ʂ� \((\pm 1)^2+(\pm 2)^2+(\pm 2)^2+0^2\) →8�ʂ� \((\pm 2)^2+(\pm 1)^2+(\pm 2)^2+0^2\) →8�ʂ� \((\pm 2)^2+(\pm 2)^2+(\pm 1)^2+0^2\) →8�ʂ� \(0^2+0^2+0^2+(\pm 3)^2\) →2�ʂ� \(0^2+0^2+(\pm 3)^2+0^2\) →2�ʂ� \(0^2+(\pm 3)^2+0^2+0^2\) →2�ʂ� \((\pm 3)^2+0^2+0^2+0^2\) →2�ʂ� |
|
�Z�O�����a�̍P����(2.5)�̏ؖ�←
\((a^2+b^2+c^2+d^2)^2\)
���̎��̓I�C���[�̎l�����P����(2.2)\(=(a^2+b^2-c^2-d^2)^2+(2ac-2bd)^2+(2bc+2ad)^2\)
\((a^2+b^2+c^2+d^2)(x^2+y^2+z^2+w^2)\)
�ɂ����āC\(x=a,y=-b,z=c,w=d\)�Ƃ����Γ�����F
\(=(ax-by-cz-dw)^2\) \(+(ay+bx+cw-dz)^2\)
\(+(az-bw+cx+dy)^2\)
\(+(aw+bz-cy+dx)^2\)…(2.2)
\((a^2+b^2+c^2+d^2)^2\)
(2.5)�̎� \(x^2+y^2+z^2=w^2\) �������� \(x,y,z,w\) �̓s�^�S���X�S�g�ƌĂ�C \(x^2+y^2+z^2=w^2\) �̉��͑S��(2.5)�̌`�ŏ����邱�Ƃ��������Ă���D\(=(a^2+b^2-c^2-d^2)^2\) \(+(-ab+ba+cd-dc)^2\)
\(+(ac-bd+ca-db)^2\)
\(+(ad+bc+cb+da)^2\)
\(=(a^2+b^2-c^2-d^2)^2+(2ac-2bd)^2+(2ad+2bc)^2\)
�e�ӂ̘a�����������̂��珇��
1��:\( 1^2+2^2+2^2=3^2=9\)
�Z�O�����a�̍P����(2.6)�̏ؖ�←2��:\( 2^2+3^2+6^2=7^2=49\) 3��:\( 1^2+4^2+8^2=9^2=81\) 4��:\( 4^2+4^2+7^2=9^2=81\) 5��:\( 2^2+6^2+9^2=11^2=121\) 6��:\( 6^2+6^2+7^2=11^2=121\) 7��:\( 3^2+4^2+12^2=13^2=169\) 8��:\( 2^2+5^2+14^2=15^2=225\) 9��:\( 2^2+10^2+11^2=15^2=225\) 10��:\( 1^2+12^2+12^2=17^2=289\) �@(2.4)�ɂ����āC\(d=0\)�Ƃ����(2.5)��������D \((a^2+b^2+c^2)^2\) \(=(a^2+b^2-c^2)^2+(2ac)^2+(2ad)^2\) |
���f�Q���̔������a�P����…(3.1)�����l�ɂ��ďؖ����邱�Ƃ��ł��邪�C�ƂĂ������v�Z�ɂȂ�̂ŁC�����ł͏ȗ�����D �@�Ȃ��C�ސ��E��ʉ��Ƃ��āC16�C32���̕����a�ɂ��Ă��P����������悤�Ɍ����邪�C2,4,8�̏ꍇ�̂ݍP�������������C����ȊO�̏ꍇ�͐������Ȃ��Ƃ���Ă���D �@�f�Q���̔������a�P����…(3.1)����I�C���[�̎l�����P�����������ɂ́C�㔼4�����~2�̕�����0��������悢�D \((a^2+b^2+c^2+d^2+e^2+f^2+g^2+h^2)\) \(\times(x^2+y^2+z^2+w^2+p^2+q^2+r^2+s^2)\)
\(=(ax-by-cz-dw\)
\(+(ay+bx+cw-dz\) \(+(az-bw+cx+dy\) \(+(aw+bz-cy+dx\)
\(-ep-fq-gr-hs)^2\)
\(+eq-fp-gs+hr)^2\) \(+er+fs-gp-hq)^2\) \(+es-fr+gq-hp)^2\)
\(+(ap-bq-cr-ds\)
\(+(aq+bp-cs+dr\) \(+(ar+bs+cp-dq\) \(+(as-br+cq+dp\)
\(+ex+fy+gz+hw)^2\)
\(-ey+fx-gw+hz)^2\) \(-ez+fw+gx-hy)^2\) \(-ew-fz+gy+hx)^2\) \((a^2+b^2+c^2+d^2)(x^2+y^2+z^2+w^2)\)
\(=(ax-by-cz-dw)^2\)
\(+(ay+bx+cw-dz)^2\) \(+(az-bw+cx+dy)^2\) \(+(aw+bz-cy+dx)^2\) |
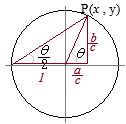 �@���̐��� \(a,b,c\) �� \(a^2+b^2=c^2\) �����Ƃ� \(\displaystyle \Big(\frac{a}{c}\Big)^2+\Big(\frac{b}{c}\Big)^2=1\) �ƕό`�ł��邩��C�_\(P(x,y)\) �� �L���� \(x=\frac{a}{c},y=\frac{b}{c}\) �����W�Ƃ���_�ɂȂ�D
�@���̐��� \(a,b,c\) �� \(a^2+b^2=c^2\) �����Ƃ� \(\displaystyle \Big(\frac{a}{c}\Big)^2+\Big(\frac{b}{c}\Big)^2=1\) �ƕό`�ł��邩��C�_\(P(x,y)\) �� �L���� \(x=\frac{a}{c},y=\frac{b}{c}\) �����W�Ƃ���_�ɂȂ�D