スマホ版は別ページ→

≪いっしょにPython≫　プログラマーの実験ノート

　このページは，プログラム言語Pythonをこれから学ぼうと考えている筆者の備忘録です．
　そこそこ調べて書いていますが，仕様を精密に調べたものではありません．どちらかと言えば，実装されたPython 3を使ってみてどうなったかということを中心に書いたものです．いわば，実験ノートの記録です．（2019.3.30，Python3.7.2に基づいて作成）
Pythonの練習には，
(1) IDLEというメニューから入って，>>>というプロンプトが表示される状態で使う場合
• 画面の上端がPython 3.7.x Shellとなっていて，２行目がFile, Edit, Shell, Debug, ...となっている
• 1行入力するたびに，エラーを確かめながら処理を進める，対話型インタプリタの形になっている
(2) IDLEというメニューから入って，左上端のFileをクリック→New Fileと進む場合
• 画面の上端がファイル名（初めはUntitled）となっていて，２行目がFile, Edit, format, Run, ...となっている
(3) Python 3.7.x という真っ黒なコマンドプロンプトの画面（ターミナルウィンドウ）から入るもの
の３通りが使えるが，以下は(2)のNew Fileから，テキストエディタを使って，プログラムを書く場合を考える．

外部パッケージnumpyのinstall

• 複数のモジュールが階層的なディレクトリに管理されているものをパッケージという．
• Pythonでは標準ライブラリに収められているモジュール以外に，外部のサイトに公開されているフリーのパッケージ，モジュールが利用しやすい．これらは外部ライブラリと呼ばれる．（パッケージやモジュールの総称として，ライブラリという用語が使われることがある．また，パッケージをさらにまとめたものという使意味に使うこともある．）
• 従来，フリーソフトと言えば，便利な代わりに玉石混交というイメージもあったが，Pythonの場合は，主にPyPI（https://pypi.org/）（パイパイ，パイピーアイ：Python Package Index）というサイトにボランティアが作ったパッケージ，モジュールが集められ，管理されていて，実績がある．
　プログラミングと言えば，真っ黒な（真っ白な）テキストエディタの画面で，何もない所から全部自分で作るというのが昔のイメージであるが，忙しい現代ではそのスタイルでは能率が悪い．Pythonでは，自分が自動車を作りたいときに「エンジン」「車体」「タイヤ」「内装」などの部品を外部パッケージからかき集めて，それらを統合したり，ない部分だけ自分で作るという仕事のスタイルがお勧めのようです．
• PyPI（https://pypi.org/）（パイパイ，パイピーアイ：Python Package Index）にあるパッケージ，モジュールは，ブラウザから選んでもよいが，（windows版）Python 3では，pipというコマンドを使えば，PyPIから目的のものを探して，インストールし，設定する作業を自動でやってくれる．
• pipを使うには，Pythonで作業中のときは，それらを全部終了して，windowsのコマンドプロンプトを出します．（windowsのメニュー画面をたどって，windowsシステムツール→コマンドプロンプトと進んでもよい．画面左下の「ここに入力して検索」という欄に，（半角文字で）cmdと書き込んでエンターキーを押してもよい．）

2. 多次元配列処理が速いnumpyのinstall

データサイエンスで必要となる多次元配列の高速処理に適したnumpyという（numerical python）Pythonのライブラリをインストールするには
【windowsのコマンドプロンプトで】
pip install numpy
と書いて，エンターキーを押す．
【数秒で】
unixのタールボールと呼ばれる圧縮ファイルがダウンロードされ，解凍，設定される．
Pythonを起動して，ファイルを読むと，/Lib/site-packagesの中に今日の日付でnumpyというフォルダが作られており，その中に必要なファイルが入っている．

(1) 配列の作成

• numpyの解説書では，numpyをインポートするときに，npという略語で表すことが多い（他の名でもよいが，他の解説を見てもすぐ分かるように，ここでもnpを使う）．
• numpyの配列は，array()，arange()メソッドなどを使って，リストやタプルから作れる．
• Javascriptの配列とは異なり，array()の頭文字は小文字で書く．
• Pythonのリストと異なり，１つの配列の各要素は同一の型と見なされる．
（int型とfloat型が混在していれば，すべてfloat型になる．文字列型と数値型が混在していれば，すべて文字列型になる．）
【例 2.1.1】array()：配列の作成
→
[ 1 -2 3]
（リストとは異なり，カンマ区切りでなく，スペース区切りになる）
→
[[ 2 3 -4 0]
[-1 0 3 1]]
（二重のリストを行ごとに入力すると，2次元配列になる）
→
[[-1]
[ 2]]
（列ベクトルは，行ごとに入力する）
【例 2.1.2】arange()：数値配列の自動作成
この配列の作り方はPythonのrange(start, stop, step)と同様になっている．
→
[0 1 2 3 4]
（引数が1つの場合，start=0, step=1として，0≦n<nの配列ができる．stopの数は省略できない．また，stopの数自体は配列に含まれないので注意）
→
[3 4 5]
（引数が2つの場合は，start,stopが与えられたものとして配列が作られる）
→
[3 5 7 9]
（引数が3つの場合は，start,stop,stepが与えられたものとして配列が作られる）
→
[3.1 5.1 7.1 9.1]
（小数でもできる）

(2) 配列のプロパティ

• 配列で使えるプロパティには，階数ndim, 要素の総数size, 形状shape，データ型dtypeがある．
• numpyでは，配列の次元数を階数（rank）と呼ぶ．（線形代数学のrankとは必ずしも一致しない）
1次元配列（階数rankは1）→
2次元配列（階数rankは2）→
3次元配列（階数rankは3）→立体になるから図示できないが，numpyでは何次元でも表せる．
[[[1 2 3]
　[4 5 6]]
[[0 1 2]
　[3 4 5]]]
赤で囲んだ[　]が一重目の配列，
青で囲んだ[　]が二重目の配列だから，
緑で囲んだ[　]は三重目の配列になる

【例 2.2.1】ndim, size, shape, dtypeプロパティ
→
[[ 1 3 5]
[ 2 -4 0]]
（a1は2次元配列≒2行3列の行列）
→
2
（階数［次元］は2）
→
6
（要素の総数は6）
→
(2, 3)
（形は2行3列型．タプルで示される）
→
int32
（32ビット整数型）
→
[2.1 5.1 8.1]
（a2は1次元配列≒1行3列の行列）
→
1
（階数［次元］は1）
→
3
（要素の総数は6）
→
(3,)
（形は1行3列型．通常タプルの末尾のカンマは省略できるが，要素数が１個の場合は末尾のカンマは省略できない．）
→
float64
（64ビット浮動小数点型）

(3) 特殊な配列の自動作成

• よく使われる配列は，あらかじめ初期化した数値で埋めて形を作っておくことができる．
• zeros()はすべての要素が0.（浮動小数点型）になっている配列を作る．
• ones()はすべての要素が1.（浮動小数点型）になっている配列を作る．
• random()は0以上1未満の乱数で埋めた配列を作る．ただし，numpyオブジェクトの下のrandomオブジェクトにある．
【例 2.3.1】zeros()メソッド
→
[[0. 0.]
[0. 0.]
[0. 0.]]
（各成分が0.0で3行2列の配列ができる）
→
[0. 0.]
（1次元で要素数がnの0.0の配列を作るには，タプルとして(n,)を書く）
【例 2.3.2】ones()メソッド
→
[[1. 1. 1.]
[1. 1. 1.]]
（各成分が1.0で2行3列の配列ができる）
→
[1. 1. 1.]
（1次元で要素数がnの1.0の配列を作るには，タプルとして(n,)を書く）
【例 2.3.3】random.rand(), random.random()メソッド
Scipy.orgのNumpyリファレンスには乱数配列の作成方法が多数示されている．ここでは，そのうちの幾つかを試してみる．
random.rand(), random.random()は，いずれも「0≦x<1上に一様分布する乱数」を発生する．
→
[[0.19247399 0.80241577 0.78714909]
[0.16684285 0.05700025 0.44348512]]
（random.rand(m,n)でm行n列の乱数配列ができる）
→
[[0.73046329 0.72967124 0.64491466]
[0.88634071 0.35886644 0.20895142]]
（内容的には同じであるが，「引数がタプル」になっており，random.random((m,n))でm行n列の乱数配列ができる）
→
[[-4.75144448 4.03309925]
[-3.27460406 -1.51720113]
[-2.73829845 -0.49334089]]
（最小値lowで幅dの区間（上端は含まない）で乱数配列を作る）
【例 2.3.4】random.randn()メソッド
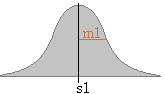s1 * np.random.randn(m,n) + m1により，平均m1，標準偏差s1の正規分布となる乱数でm行n列の配列を作る．
統計で習うように，左図のように平均付近が濃い帽子型（富士山型）の分布になる．［一様分布ではない．］
→
[[54.26774667 62.69119258]
[51.88419979 50.37520617]
[40.02619633 48.75547132]]
（この例のような要素数が6個程度では，実際に正規分布に近いのかどうかは確かめられないが，要素数を100個程度に増やして分布を調べてみると，ほぼ正規分布に近いものになっていることが分かる）

(4) 配列形状の変更

• numpyの配列は，一旦作られてから，後で形状を変えることができる．ただし，要素の総数が変わる変更はできない．
• 配列形状の変更は，関数reshape()でも，配列のメソッドreshape()でもできるが，引数が異なる．いずれも，新しい配列が返され，元の配列に上書きしない限り元の配列も残る．
• numpyの配列プロパティ，ndimやsizeは左辺値として代入できないが，shapeは左辺値としてタプルを代入して書き換えできる．ただし
配列.shape = タプル
の形でshapeを書き換えると，元の配列が変わってしまう．
【例 2.4.1】reshape()：関数，配列.reshape()：メソッド，配列.shape=タプル：プロパティに代入
→
[3 4 5 6 1 2]
（形状変更後も元の配列はある）
→
[[3 4 5]
[6 1 2]]
（1×6→2×3の形状変更をreshape()関数で行う場合，第1引数を元の配列にして，第2引数を形を表すタプルにする）
→
[[3 4]
[5 6]
[1 2]]
（2×3→3×2の形状変更．要素総数が等しければできる）
→
[[3]
[4]
[5]
[6]
[1]
[2]]
（列ベクトルにすることも可能）
→
[[3 4 5]
[6 1 2]]
（配列a4のコピーができるのでなく，a4の形が変わる）

(5) 配列要素の参照

• numpyの配列は個別に参照できる．
【例 2.5.1】配列[m,n]
→ 7
（L1はPythonのリスト．要素を示すには[]が次元の数だけ必要）
→ 7
（a1はnumpyの配列．リストの参照と似ているが，要素を示すには１つの括弧の中でカンマで区切る）
【例 2.5.2】配列[m,n]=x 左辺値として代入して書き換えることができる
→
[[ 3 4 5]
[ 6 1 -3]
[ 7 8 9]]
【例 2.5.3】　リストと同様に，スライスの方法が使える
スライスは[start:stop:step, ...]で指定し，start≦n<stopの区間を増分stepで拾っていく．
→
[[0 1]
[7 8]]
（配列要素の読み出し．0番スタートで，a1[1行目からあと全部,2列目の前まで]→a1[1～2行目,0～1列目]）
→
[[ 3 -1 -1 6]
[ 0 -1 -1 3]
[ 7 8 9 10]]
（配列要素の書き換え．0番スタートで，a1[0行目から1行目,1列目から2列目まで]を-1にする）
→
[[ 3 -1 -1 6]
[ 0 0 -1 3]
[ 0 0 9 10]]
（配列要素の書き換え．0番スタートで，a1[1行目から2行目,0列目から1列目まで]を0にする）

(6) 配列の和，差，定数倍，1次結合

• Pythonで普通に使われるリストやタプルで，各要素を定数倍したり，対応する要素の和差を求めるためには，forなどのループを使って，個々の要素をスクリプトで「なめていく」という方法を取らざるを得ず，（数千行×数千列など）データが大きくなると，計算が遅くなると言われています．
• また，次の例2.6.1～2.6.2に示すように，リストやタプルを単純に定数倍したり，和差を求めると，意図したものとは異なるものができます．
【例 2.6.1】　Pythonの普通のリストの定数倍は，同じリストの繰り返しを作る．和はリストをつないだものになる．
→
[[3, 4, -5], [0, -1, 2], [3, 4, -5], [0, -1, 2]]
（リストの2倍は，リストを2回繰り返したものになる。3倍なら3回繰り返すだけ）
→
[[3, 4, -5], [0, -1, 2], [1, -2, 3], [6, 7, -8]]
（リストの和は，２つのリストをつなぐだけ）
→ エラー
（リストの差は定義されないから､エラーになる）
【例 2.6.2】　Pythonの普通のタプルの定数倍は，同じタプルの繰り返しを作る．和はタプルをつないだものになる．
→
((3, 4, -5), (0, -1, 2), (3, 4, -5), (0, -1, 2))
（タプルの2倍は，タプルを2回繰り返したものになる。3倍なら3回繰り返すだけ）
→
((3, 4, -5), (0, -1, 2), (1, -2, 3), (6, 7, -8))
（タプルの和は，２つのタプルをつなぐだけ）
→ エラー
（タプルの差は定義されないから､エラーになる）
• 以上のような，Pythonで普通に使われるリストやタプルとは異なり，配列計算に優れているnumpyでは，配列を定数倍したり，和差を求める計算が簡単にでき，かつデータが大きくなっても高速にできます．
【例 2.6.3】　numpyの配列を定数倍すると，各要素を定数倍した配列になる．numpyの配列の和差は各要素の和差を要素とする配列になる．
→
[[ 2 4 6]
[ 8 10 12]]
（numpy配列を2倍すると，各要素を2倍した配列になる．数学の行列計算と同じ）
→
[[1 3 2]
[6 5 4]]
（numpy配列とnumpy配列を足すと，各要素を足した配列になる．数学の行列計算と同じ）
→
[[1 1 4]
[2 5 8]]
（numpy配列からnumpy配列を引くと，各要素を引いた配列になる．数学の行列計算と同じ）
→
[[2 3 4]
[5 6 7]]
（numpy配列に定数を足すと，各要素に定数を足した配列になる．数学の行列計算において，+定数×ones()としたものと同じ）
• ２つの配列が等しいかどうかは
配列1 == 配列2
により，各要素ごとに，等しければTrue，等しくなければFalseで示されます
【例 2.6.4】
→
[[ True True]
[False True]
[ True True]]

(7) 配列の積

• 数学でのベクトル，行列の積は次のように定義されます．
［ベクトルの内積］
(1) 要素数が等しい２つの行ベクトルの内積（ドット積）は

（対応する要素の積の和になる=productのsumになる=SumProductになる）
　要素数が等しくなければ，内積（ドット積）は定義されない．
(2) 要素数が等しい２つの列ベクトルの内積（ドット積）も同様にして

（対応する要素の積の和になる=productのsumになる=SumProductになる）
　要素数が等しくなければ，内積（ドット積）は定義されない．
(3) m×k型の行列Ａとk×n型の行列Ｂの積Ｃは，Ａの列数とＢの行数が等しい（=k）ときに限り定義され，Ａのi行とＢのj列の積がCの(i,j)成分となる．Ｃはm×n型になる．
• numpyにおける配列の積は，多様な計算に対応するためか，もっと広く定義されます．ただし，次のように２つの配列の型に応じて，場合分けして定義されている．（統一的な１つの演算というよりは，型ごとに対応する演算が決まる「ハイブリッド型の混成部隊」のような感じ）→引用元の文書（英語）
【用語の注意】
• 数学ではのような平面ベクトルを2次元ベクトル，のような空間ベクトルを3次元ベクトルという．これは，列ベクトルで表して，，とする場合も同様である．
　要するに，数学のベクトルの次元とは，要素の個数のことになる．
　これに対して，配列ではは1次元配列，は2次元配列という．（配列のブラケット[　]が二乗になっている）
　も2次元配列という．
• 数学では行列の階数（rank）とは，1次独立なベクトルの個数で，の階数は3，
　の階数は2である．
　これに対して，配列ではの階数は2，
　の階数も2である．
• 以上のように，行列や配列を扱う場合には，用語が紛らわしいので，以下においては配列の形状（shape）を中心に考えることにする．
　この形状（shape）は，numpyのエラーメッセージで
ValueError: shapes (2,3) and (2,3) not aligned: 3 (dim 1) != 2 (dim 0)
のように，エラーのポイントとして表示される重要な目印なので，形状（shape）で考えると分かり易い．
• 上記の例では，各々の配列の形状（shape）は，v→(2,)，w→(3,),V→(2, 1), W→(3, 1), a→(3,), b→(2, 3), c→(3, 1), M→(3, 3), N→(3, 2)であり，
　数字が２つあるV, W, b, c, M, Nは(行数, 列数)を表し，数字が１つのv, w, aは(列数,)になっている．…shapeはタプルで表され，タプルは末尾のカンマを略してもよいが，要素が１つしかないタプルは(n)のように書くと，Python上でタプルと評価されずに単なる数として扱われるから，要素が1つの場合だけは末尾のカンマを省略できない．
　もちろん，配列が三重になると立体に積み上げたレンガのような形状を想定することになり，高さも必要になる．四重以上になると，見える形にはできないが，プログラム上は単に[　]が四重，...になるだけで，問題なく簡単に表せる．
　[[[1,2],[3,4]],[[5,6],[7,8]]]←三重の配列：shapeは(2,2,2)，
　[[[[1,2],[3,4]],[[5,6],[7,8]]],[[[9,10],[11,12]],[[13,14],[15,16]]]]←四重の配列：shapeは(2,2,2,2)
【要点】
配列の形状が(n,)のように数字1つのときは，横1列になっている．
配列の形状が(m,n)のように数字2つのときは，(m行,n列)になっている．
配列の形状が(k,m,n)のように数字3つのときは，三重になっているが，最後のnは列数，最後から2番目のmは行数と考えてもよい．kは一番外側の[　]の中にある，最も大きな[　]の区切りの個数．
(1) 配列形状が(n,)のaとbで要素数nが等しいとき，np.dot(a,b)はaとbの内積を返す．
【例 2.7.1】
→
a*x + b*y + c*z
（行ベクトルと行ベクトルをdot()メソッドで掛けると，ベクトルの内積として１つの数になる）
※
（なお，配列と定数を演算子 * で掛けると，配列の各成分を定数倍した配列になる．
d1 * x → [a*x b*x c*x] ）
（また，配列と配列を演算子 * で掛けると，対応する要素の積から成る配列になる．型が異なればエラー
d1 * d2 → [a*x b*y c*z] ）
※列ベクトルは，配列としては(n,1)型であるので，取り扱いが異なり，列ベクトルと列ベクトルのdot()積は定義されない．
d1 = np.array([[a],[b],[c]])
d2 = np.array([[x],[y],[z]])
d3 = np.dot(d1, d2) → エラー
(2) 配列aの形状が(m,k)で配列bの形状が(k,n)である場合，np.dot(a,b)は数学における行列の積abに等しい．
左（前）の配列の列数と右（後）の配列の行数が等しいときに限り，np.dot(a,b)が定義され，結果は(m,n)型になる．
(m,k)と(k,n) → (m,n)　しりとりの仕組み
【例 2.7.2】
→
[[a*p + b*r + c*t a*q + b*s + c*u]
[p*x + r*y + t*z q*x + s*y + u*z]]
(2,3)型.(3,2)型→(2,2)型

→
[[a*p + q*x b*p + q*y c*p + q*z]
[a*r + s*x b*r + s*y c*r + s*z]
[a*t + u*x b*t + u*y c*t + u*z]]
(3,2)型.(2,3)型→(3,3)型

※なお，この型の配列の積は，数学における行列の積に等しくなるが，数学における行列の積が定義できるときはいつでも配列の積もそれに等しいとは限らない．
d5 = np.array([a,b,c]) →(3,)型
d6 = np.array([[x],[y],[z]]) →(3,1)型
np.dot(d5,d6)は[a*x + b*y + c*z] →(1,)型の配列で次の行列の積と一致する．
np.dot(d6,d5)はエラーになる．しかし，行列計算では，[3×1]型.[1×3]型→[3×3]型

　これは，d5が(3,)型，すなわち[　]が一重だから，(m,k)型.(k,n)型の定義に当てはまらないと評価している可能性がある．
• numpyにおける配列の積では，最終軸上の積の和（a sum product over the last axis of a and b），aの最終軸およびbの後ろから2番目の軸上の積の和（a sum product over the last axis of a and the second-to-last axis of b）など，「軸上の積の和」という用語が出てきます．筆者の解釈では，これは次の意味です．
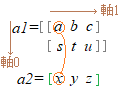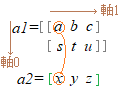　左図のような(2,3)型配列a1があるとき，最も大きな区切りは行で，これを軸0とする．列の区切りは細かい方になり，これを軸1とする．このように(2,3)配列では，軸0と軸1の２つの軸がある．
　２つの配列a1:(2,3)型とa2：(3,)型について，最後軸はいずれも列で，列数は3個で等しい．
　このとき「最終軸上の積」とは，最終軸に沿って掛けて行き，積a*x, b*y, c*z, s*x, t*y, u*zの和 a*x+b*y+c*z　s*x+t*y+u*zを求めるから，最終軸の次元が１つ減り，できる配列は1次元：(2,)になる．
　引数の順序を変えた場合，積は定義されていない（可換ではない）
(3) 配列aの形状が(m,k)で配列bの形状が(k,)である場合，np.dot(a,b)は最終軸上の積の和になる．
【例 2.7.3】
→
[a*x + b*y + c*z p*x + q*y + r*z]
（(2,3)型.(3,)型→(2,)型になる）
※print(np.dot(d2,d1))はエラーになる
※傍から見ると，順序を逆にした積を定義しなかった理由は，必ずしも理解しやすいものではないが，次のような計算が多い，少ないに応じて定義するかしないかを分けたのかもしれない．
　(トマト,りんご,ミカン)の1号店，2号店の売上個数がd1 = [[a,b,c],[p,q,r]]個で，(トマト,りんご,ミカン)の順に単価がd2=[x,y,z]円のとき，上記のnp.dot(d1,d2)は店舗ごとの売り上げ合計になる．この計算は多いが，逆順のかけ算np.dot(d2,d1)は少ないのかも？
(4) 配列aの形状が(p,q,r)で配列bの形状が(r,s)である場合，np.dot(a,b)はaの最終軸とbの後ろから2つ目の軸上の積の和になる．
（rの要素数が一致する場合に，(q,r).(r,s)で行列の積を作り，その束をp行並べる）
【例 2.7.3】
→
[[[a*p + b*r + c*t a*q + b*s + c*u]
[d*p + e*r + f*t d*q + e*s + f*u]]

[[g*p + h*r + i*t g*q + h*s + i*u]
[j*p + k*r + l*t j*q + k*s + l*u]]]


これら２つを束にして書いたものになっている．
この結果は，(p,q,r)型と(r,s)型の積を求める代わりに，(p×q,r)型と(r,s)型の行列として積(p×q,s)型を求めておいて，その結果を(p,q,s)型に直したものと等しい．
→
[[[a*p + d*q b*p + e*q c*p + f*q]
[g*p + j*q h*p + k*q i*p + l*q]]

[[a*r + d*s b*r + e*s c*r + f*s]
[g*r + j*s h*r + k*s i*r + l*s]]

[[a*t + d*u b*t + e*u c*t + f*u]
[g*t + j*u h*t + k*u i*t + l*u]]]








これら３つを束にして書いたものになっている．

(8) 行列と連立方程式

• Pythonにおいて，行列や線形代数を扱うには,sympyをインポートする方法もある．
• 以下においては，大きな行列の高速処理に適したnumpyを使う方法を調べる．
ⅰ) 行列式の計算
• munpyの中にlinalg（linear algebraの略）というモジュールがあって，そこに多くのメソッドが定義されている．
• 行列式の値は，np.linalg.det(正方行列)で求められる．
【例 2.8.1】
→
-2.0
11.000000000000002
numpy.linalg.det()では，行列式の値を浮動小数点で求める．実際には，この例の行列式の値は−2と11であるが，小数第15位付近の丸め方によって微妙に誤差を生じることがある．
ⅱ) 逆行列の計算
• munpyの中にlinalg（linear algebraの略）というモジュールがあって，そこに多くのメソッドが定義されている．
• 行列式の値は，np.linalg.inv(正方行列)で求められる．
【例 2.8.2】
→
[[-5.28455285 1.70731707]
[ 3.49593496 -0.97560976]]
結果は浮動小数点で示される．小数の丸め方によって微妙に誤差を生じることがある．
→
[[ 0.23241464 0.21801728 0.05758947]
[ 0.36610448 0.43192102 -0.26326615]
[-0.91628959 -0.35067873 0.23755656]]
ⅲ) 行列の累乗
• munpyの中にlinalg（linear algebraの略）というモジュールがあって，そこに多くのメソッドが定義されている．
• 行列の累乗は，np.linalg.matrix_power(正方行列,n)で求められる．nは正の整数の場合は正方行列をn回掛けたもの，負の整数の場合はその逆行列，0の場合は単位行列になる
【例 2.8.3】
→
[[ 6 -5]
[ 5 -4]]

→
[[-4. 5.]
[-5. 6.]]

負の指数の場合は，各要素を浮動小数点数で表される．
→
[[1 0]
[0 1]]
零乗は単位行列になる．
ⅳ) 連立方程式の解
• numpyの中にlinalg（linear algebraの略）というモジュールがあって，そこに多くのメソッドが定義されている．
• 連立方程式の解は，np.linalg.solve(係数行列,右辺の定数ベクトル)で求められる．
• np.linalg.solve()で解くとき，「係数行列が正方行列でない場合」「係数行列が正則でない場合=行列式が0になる場合=逆行列が存在しない場合=不能解，不定解になる場合」「文字係数になっている場合」はエラーとして処理される．
• 係数行列Ａがn×n行列の場合，数学では未知数Ｘ，右辺Ｐともn×1行列（列ベクトル）でなければならないが，np.linalg.solve()では，右辺Ｐが行ベクトル（1×n行列）の場合にも，右辺の形に合わせて解が示される. 【例 2.8.4】
→
[ 2. -3.]
右辺の定数行列を(n,)型の配列で与えると，結果も(n,)型で示される．
なお，右辺の定数行列をq1 = np.array([[-2],[7]])のように(n,1)型の配列で与えると，結果も(n,1)型で示される．
[[ 2.]
[-3.]]
→
[3. 1. 2.]
未知数が3個以上の場合も同様
○== メニューに戻る ==