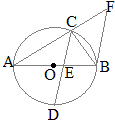
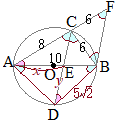
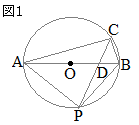
|
���O�p�`�̑������� �@����(1)(2)(3)�͎O�p�`�����������ƌĂ�Ă���C���̂����P�ł����藧�ĂQ�̎O�p�`�������ɂȂ�D �@�t�ɁC�Q�̎O�p�`�������ł���Ƃ��C����(1)(2)(3)�͂��ׂĐ��藧�D
�y�v�_�z
(1)�@�Q�g�̊p�����ꂼ�ꓙ����
(2)�@�R�g�̕ӂ̔䂪���ꂼ�ꓙ���� (3)�@�Q�g�̕ӂ̔�Ƃ��̊Ԃ̊p�����ꂼ�ꓙ���� 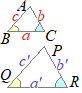 �i����j
�i����j(1)�@�O�p�`�̓��p�̘a��180��������u2�g�̊p�����ꂼ�ꓙ�����v�Ƃ��C�u3�g�̊p�����ꂼ�ꓙ�����Ȃ�v �@�����ł��邱�Ƃ��ؖ�����ɂ́u2�g�v�������Ώ\�����Ƃ������� �@�E�}�ł���B=��Q, ��C=��R�������C��A=��P�͎����I�ɐ��藧�D  (2)�@�u3�g�̕ӂ̔䂪���ꂼ�ꓙ�����v�Ƃ����������͂Q��ނ���D
(2)�@�u3�g�̕ӂ̔䂪���ꂼ�ꓙ�����v�Ƃ����������͂Q��ނ���D�@�P�� a:a'=b:b'=c:c' …(*1) �̂悤�� �i�������̐}�`�j:�i�������̐}�`�j �̏��ɂR�g���ׂ���@ �@������́C�A��̏������� a:b:c=a':b':c' …(*2) �̂悤�� �i��������1�j:�i��������2�j:�i��������3�j =�i��������1�j:�i��������2�j:�i��������3�j �̏��ɂQ�g���ׂ���@ �@�����̕��@�̂����C(*1)�̏������� �Ƃ��������ɒ����܂����C(*2)�̘A������̏���������͂��̂悤�Ȕ�̒l�Ƃ����l�����͂ł��܂���D �@��̒l�m�����̌`�n�ɒ����ɂ́C(*1)�̕����L���ł��D |
 (3)�@�u�Q�g�̕ӂ̔�Ƃ��̊Ԃ̊p�����ꂼ�ꓙ�����v�Ƃ́C�E�}�̗�ł�
(3)�@�u�Q�g�̕ӂ̔�Ƃ��̊Ԃ̊p�����ꂼ�ꓙ�����v�Ƃ́C�E�}�̗�ł�a:a'=b:b' …(*3) ��C=��R �Ȃǂł��D �@���̂����́u�ӂ̔�v�̕����� a:b=a':b' …(*4) �Ə������Ƃ��ł��܂��D�i�������ab'=ba'�ɑΉ����Ă���C�����W��\���j �@�������C(*3)�̕����u������v�ɑΉ����Ă���C�ʐϔ�̖��ւ̉��p���y�Ȃ̂�(*3)�̕����L�����ƍl�����܂��D�i�M�҂̎茳�ɂ��钆�w�Z�̋��ȏ��͂������(*3)�̌`�ŏ�����Ă��܂��j
�y�v�_�z
�ӂ̔�� �i�������̐}�`�j:�i�������̐}�`�j a:a'=b:b' …(*3) �̏��ɕ��ׂ�̂��W���I ���ꂼ��̐}�`�őΉ�����ӂ̏��ɏ����Ă��悢 a:b=a':b' …(*4) |
 (1)�@
(1)�@ (2)�@
(2)�@
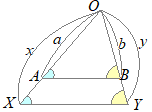
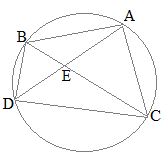
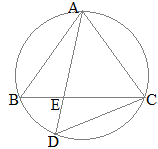
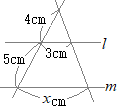
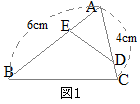 �@�}�P�̂悤��
�@�}�P�̂悤��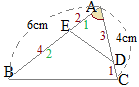
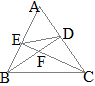
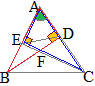
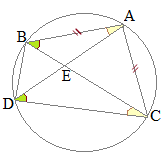
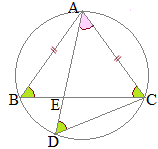
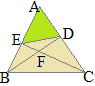 (*3)(*4)�ɂ��C
(*3)(*4)�ɂ��C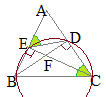
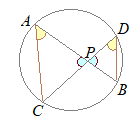
 �@
�@
 �@
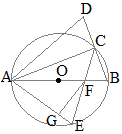
�@
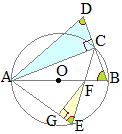
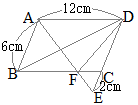
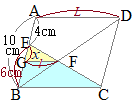
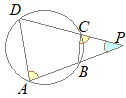
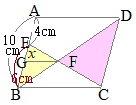 �i�ʉ��j
�i�ʉ��j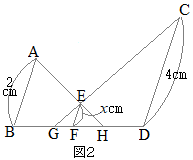
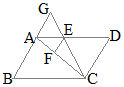
 ����ɂ��
����ɂ��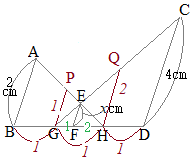 �i�ʉ��j
�i�ʉ��j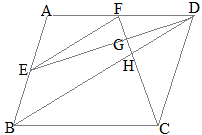
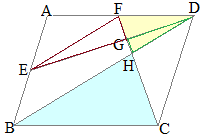
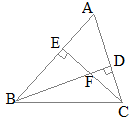
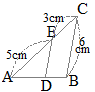
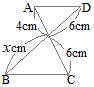
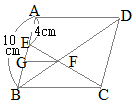
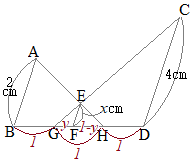
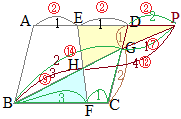 ���ȉ��C�}���̐����́u��v�ł��邪�C������́Z�����͘A�䂪�����悤�ɒ����ς݂̐����Ƃ���
���ȉ��C�}���̐����́u��v�ł��邪�C������́Z�����͘A�䂪�����悤�ɒ����ς݂̐����Ƃ���
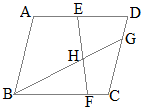
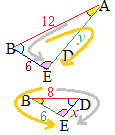 ����ɂ��C
����ɂ��C