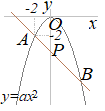|
�y�l�����P�z
�Z�O�p�`�̖ʐς́C���w�Z�̂Ƃ�����g���Ă������ �ŋ��߂邱�Ƃ��ł��܂��D 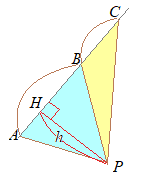 �Z�E�̂悤�Ȑ}�`�ɂ����āC ��PAB����PBC�̖ʐϔ�����߂����Ƃ�
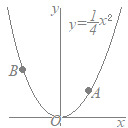
�Z�E�̂悤�Ȑ}�`�ɂ����āC ��PAB����PBC�̖ʐϔ�����߂����Ƃ�AB��BC�����ꂼ��̎O�p�`�̒�ӂɑI�ԂƁC����PH=h�����ʂɂȂ�̂� ��PAB:��PBC = : =AB:BC �ˁ@���������ʂȂ�C�O�p�`�̖ʐϔ�͒�ӂ̒����̔�ɓ����� 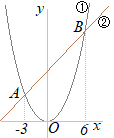 �y���P�z
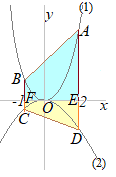
�y���P�z�@�E�̐}�ŁC�@�͊�
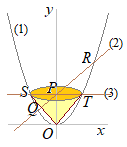
(1)�@��
(2)�@�萔a, b�̒l�����߂�B (3)�@����AB��ɓ_P���Ƃ�C��OAP�̖ʐς���OPB�̖ʐς̂Q�{�ƂȂ�悤�ɂ������B���̂Ƃ��_P�̍��W�����߂�B �i���m��2000�N�������j
(2)�@�_A, B��
A�@�F�@x=−3�̂Ƃ��C
����y=ax+b�͂Q�_A, B��ʂ邩��B�@�F�@x=6�̂Ƃ��C ���������āCA(−3, 6), B(6, 24)
A�@�F�@6=−3a+b…(i)
B�@�F�@24=6a+b…(ii) ���̘A��������(i)(ii)�������āCa, b�����߂�D (ii)−(i) 18=9a a=2 �����(i)�ɑ������ƁCb=12 y=2x+12…�i���j 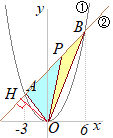 (3)
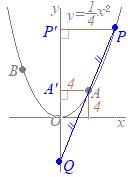
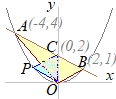
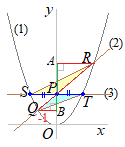
(3)��OAP����OPB�̖ʐς��v�Z����Ƃ��ɁC��AP, BP���ӂɑI�ԂƁC�E�}�̂悤�ɍ���OH�͋��ʂɂȂ蓙�����D ���̂Ƃ��C��OAP����OPB�̖ʐϔ�͒��AP, BP�̒����̔�ɂȂ�D 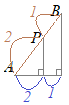 �E�}�̂悤�ɏc���Ɖ������Ђ��ƁC�����}�`�̐������牡�����Ȃ킿x���W�̍���2 : 1�ɂȂ�D
�E�}�̂悤�ɏc���Ɖ������Ђ��ƁC�����}�`�̐������牡�����Ȃ킿x���W�̍���2 : 1�ɂȂ�Dx���W�� A(−3) → P(3) → B(6) �Ƃ����x���W�̍���6:3=2:1�ɂȂ�D P��y=2x+12��ɂ����āCx=3������ y=2×3+12=18 P(3, 18)…�i���j |
�����̖��͋L�q�����ł����C��������ł̓ǎ҂̑��쐫���悭���邽�߂ɁC���̃T�C�g�ł́C�Ǝ��ɑI����ɂ��Ă��܂��D�I�����̒����琳�������̂��P�N���b�N���Ă��������D����I�����ɋ^�₪����Ƃ��́C������҂�ς킷���ƂȂ��C���̃T�C�g�̊Ǘ��l�Ɏ��₵�Ă��������D
 �y���P�z
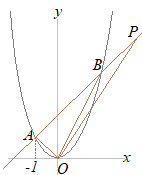
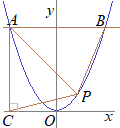
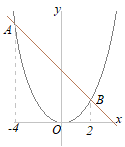
�y���P�z�@�E�̐}�ŁC�Ȑ���y=x2�̃O���t�ł���C�O���t��ɁCx���W��−1�ł���_A���Ƃ�܂��B�_A��ʂ�X��1�̒����ƋȐ��Ƃ̌�_��B�Ƃ��C����AB��ɁCx���W�����ł���_P���Ƃ�܂��B �@��OAB����OBP�̖ʐς��������Ƃ��C�_P�̍��W�����߂Ȃ����B �i��ʌ�2000�N�������j
�_A�͋Ȑ�y=x2��̓_������x=−1�̂Ƃ�
y=(−1)2=1 �_A�̍��W��(−1, 1)�ɂȂ邩��C���̓_A��ʂ�X��1�̒����̎���y=x+b�Ƃ����� 1=−1+b b=2 ����AB�̎���y=x+2�ɂȂ�D B�̍��W�́C���̘A���������̉��ɂȂ�D y=x+2…(ii) 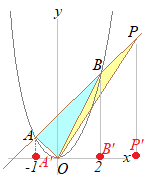 y�����������x2=x+2
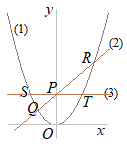
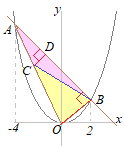
y�����������x2=x+2x2−x−2=0 (x+1)(x−2)=0 x=−1, 2 x=−1�͓_A��\������C�_B��x=2 �@�E�}�ɂ�������OAB����OBP�̖ʐς��������Ƃ��CAB��BP�����ꂼ��̎O�p�`�̒�ӂɑI�ԂƁC�����͋��ʂɂȂ邩��C��ӂ̒�����AB=BP�ɂȂ�D �@���̂Ƃ��C���w�Z�Q�N���ŏK�������s���̐�������C�}��A'B'=B'P'�����藧�D A'����B'�܂�3�i�ނ���CB'����P'�܂�3�i�ނ�P'=5 (ii)��x=5���������y=7 P(5, 7)…�i���j |
 �@�u�_
�@�u�_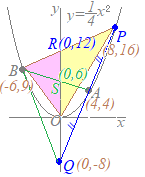
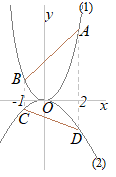
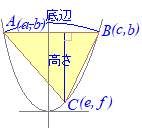
 �@��`�̖ʐς��i���+����j�~������2 �ŋ��߂��܂��D
�@��`�̖ʐς��i���+����j�~������2 �ŋ��߂��܂��D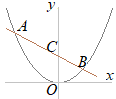
 �@����
�@����
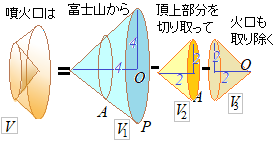
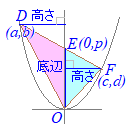
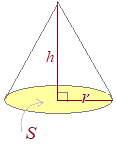 �y�~���̑̐ς̌����z
�y�~���̑̐ς̌����z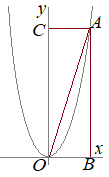
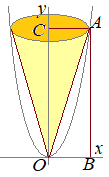 �i�j
�i�j