|
�y�v�_1.1�z��~���̑��ʐρ�
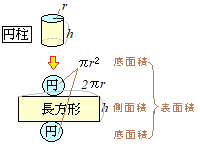 ���~���̕\�ʐς́C�Q�̒�ʐςƑ��ʐς̘a�ɂȂ�܂��D
���~���̕\�ʐς́C�Q�̒�ʐςƑ��ʐς̘a�ɂȂ�܂��D���E�}�̂悤�ɒ�ʂ̔��a��r�C������h�ł���~���̑��ʂ͒����`�ŁC���ʐς� 2��r×h �ɂȂ�܂��D
���ȉ��Ɉ��p���Ă���������ŁC���̖��͋L�q���ł����C���̋��ނł�Web��ł̑��쐫���悭���邽�߂ɁC�I����ɂ��Ă��܂��D
�܂��ꓖ����ł͗͂��t���܂���̂ŁC�v�Z�p���Ȃǂ��g���ď\���l���Ă���C�I�������N���b�N���Ă��������D ����C�̓_���ʂƉ�����o�܂��D |
 �y1.1 �~���̑��ʐρz
�y1.1 �~���̑��ʐρz
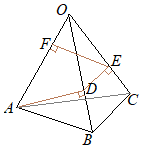
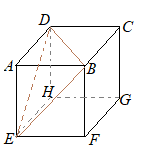
�@�E�̐}�̒����`���C����l�����Ƃ��ĂP��]�����Ƃ��ɂł��闧�̂̑��ʐς����߂Ȃ����B
�@�������C�~���������Ƃ���B �i�Ȗ،�2000�N�������j
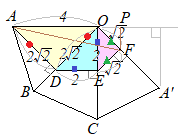
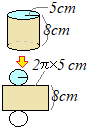 �W�J�}��`���ƁC�E�}�̂悤�ɑ��ʂ͏c�̒�����8 cm�C���̒������i��ʂ̉~���̒����j2�~5 cm�̒����`�ɂȂ邩��C���̖ʐς�
�W�J�}��`���ƁC�E�}�̂悤�ɑ��ʂ͏c�̒�����8 cm�C���̒������i��ʂ̉~���̒����j2�~5 cm�̒����`�ɂȂ邩��C���̖ʐς�8×2�~5=80��(cm2)…�i���j |
 �y�v�_1.2�z��~���̑��ʐρ�
�y�v�_1.2�z��~���̑��ʐρ�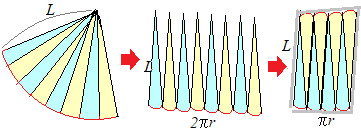

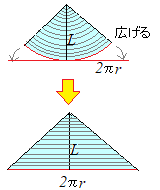 �ʂ˂��`�ɐ��āC����L���Ă����ƍl����D
�ʂ˂��`�ɐ��āC����L���Ă����ƍl����D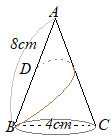
 �y�v�_2�z
�y�v�_2�z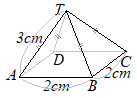
 �����`
�����`
 ��ʂ�
��ʂ�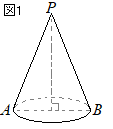
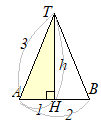
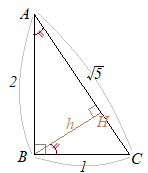
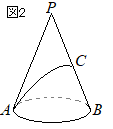 (2)�@����
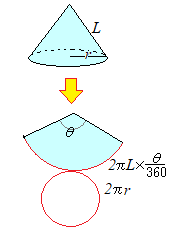
(2)�@���� (2)�@��ʂ̔��a��
(2)�@��ʂ̔��a��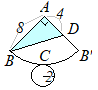 ���ʂ̓W�J�}�͐�^�ɂȂ�C���̒��S�p��
���ʂ̓W�J�}�͐�^�ɂȂ�C���̒��S�p��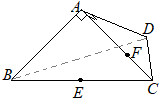
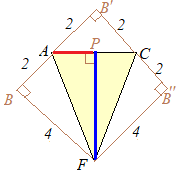
 �E�}�̂悤��
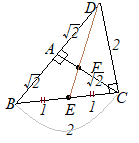
�E�}�̂悤��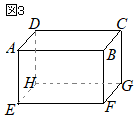
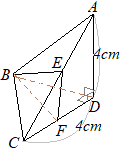
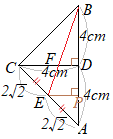
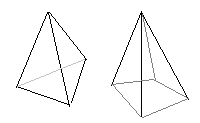
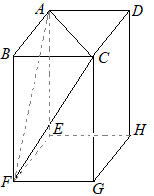
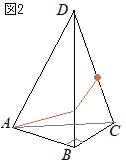
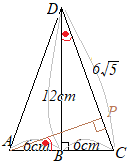
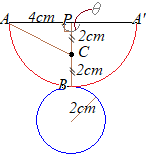
 (3)�@���̒����̂ɂ����āC�}�T�̂悤�ɁC��
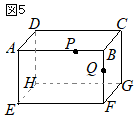
(3)�@���̒����̂ɂ����āC�}�T�̂悤�ɁC��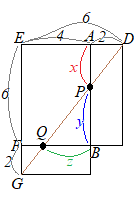 �@�E�}�̓W�J�}�ɂ����āC
�@�E�}�̓W�J�}�ɂ����āC