規則性

■規則性の発見

□　以下の内容は、結果を覚えても意味がありません。規則性を見つけるという訓練です。
□　考え方の例は示していますが，このように考えなければならないことはなく，考え方は他にも何通りもありえます。
□　以下の問題では，「目で計算」できる10番以下でなく，「初めの２，３番」→「規則性の発見」→「問題解決」という思考経過をたどるようにやや大きめの数字として20番目としましたが，この20という数字には特に意味はなく，問題としては10番目でも100番目でもかまいません。

【例１】
右のように点が並んでいるとき，第20番目には何個の点がありますか。

【考え方】
3番目は3×3＝3²
4番目は4×4＝4²
・・・
20番目は20×20＝20²＝400・・答

【例2】
右のように点が並んでいるとき，第20番目には何個の点がありますか。

【考え方】
右下の図のように同じ数の点を逆向きに組み合わせると，
3番目は3列×4行＝12
4番目は4列×5行＝20
・・・
20番目は20列×21行＝420

その半分だから210・・答

【例3】
右の図で第20番目の図形には

の棒が何本使われていますか。

【考え方】
右下の図のように縦棒と横棒に分けて考えると，
3番目は縦横とも3(3+1)=12 → 12×2=24
4番目は縦横とも4(4+1)=20 → 20×2=40
・・・
20番目は縦横とも20(20+1)=420 → 420×2=840・・答

■問題

１右のように点が並んでいるとき，第20番目には何個の点がありますか。個［解説］次のように見ると第4番目で3×4　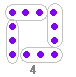また，次のように見ると4番目で4²-2² ⇒ 76
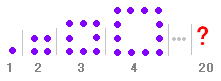
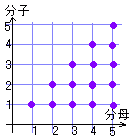
２右のように点が並んでいるとき，第20番目には何個の点がありますか。個［解説］第5番目では4×3個 ⇒ 57
３右の図で第20番目には何本の棒が使われていますか。本［解説］上の例2の３倍になります。 ⇒ 630
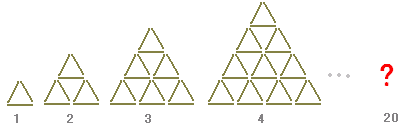
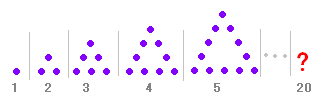
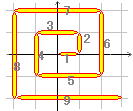
４右図のようにｘｙ平面上で，原点から出発してｘ，ｙ座標が整数となる点を順にたどる。左折するまでの線分の長さは第１番目は１，第２番目は１，第３番目は2・・・などとなっています。第20番目の線分の長さは幾らですか。［解説］長さは順に１，１，２，２，３，３，・・・となっています。 ⇒ 10
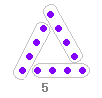
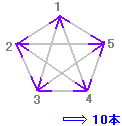
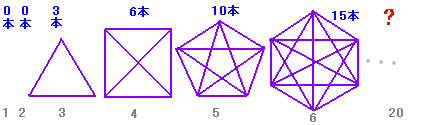
５正20角形の頂点を結んでできる線分（辺と対角線の総数）［解説］五角形を例にとると，どの頂点からも自分以外の頂点へ線が出ています：4本×5。しかし，そのように数えるとどの線も２回ずつ数えたことになりますので　÷2で10 ⇒ 190
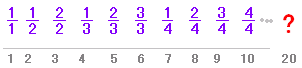
６右の分数で第20番目の分数の分母と分子の和は［解説］分母が4の分数の終りまでには１＋２＋３＋４＝10個あります。（上の例２参照）分母が5の分数の終りまでには15個分母が6の分数の終りまでには21個だから，分母が6の分数の5番目の分数は何かと考えます。参考：次の点の数は例２で求めています。 ⇒ 11

●==メニューに戻る