比例・反比例.入試問題

大きな区分

現在地と前後の項目

*** 比例 ***/比例/比例のグラフ1/比例のグラフ2/比例のグラフ3/*** 反比例 ***/反比例/反比例のグラフ1/反比例のグラフ2/反比例の式/*** 反比例の応用 ***/てこ1/てこ2/てこ3/*** 比例.反比例まとめ ***/比例と反比例のグラフ1/比例と反比例のグラフ2/表→関係式1/表→関係式2/文章→関係式/データとグラフ/比例.反比例(入試問題)/

== 比例・反比例（入試問題） ==
【例題１】

yはxに比例し，x=3のとき，y=12である。このとき，yをxで表せ。

（長崎県2015年入試問題）

（解答）
yがxに比例するとき
y=ax（aは定数）
とおける．
x=3のとき，y=12であるから
12=a×3
a=4
したがって
y=4x…（答）

※以下に引用する高校入試問題で，元の問題は記述式の問題ですが，ｗｅｂ画面上で入力問題にすると操作性が悪いので，選択問題に書き換えています．

【問題１】　（画面上で解答するには，選択肢の中から正しいものを１つクリック）

(1)
yはxに比例し，x=1のときy=4である。x=−2のときのyの値を答えなさい。

（新潟県2015年入試問題）

解説やり直す

y=4 y=8 y=−4 y=−8

yがxに比例するとき
y=ax（aは定数）
とおける．
x=1のとき，y=4であるから
4=a×1
a=4
このとき
y=4xと書けるから
x=−2のとき，y=4×(−2)=−8 …（答）

→閉じる←

(2)
yはxに比例し，x=12のときy=−8である。x=−3のときのyの値を求めなさい。

（島根県2017年入試問題）

解説やり直す

y=2 y=3 y=−4 y=−6

yがxに比例するとき
y=ax（aは定数）
とおける．
x=12のとき，y=−8であるから
−8=12a
$a=-\frac{8}{12}=-\frac{2}{3}$
このとき
$y=-\frac{2}{3}x$ と書けるから
x=−3のとき $y=-\frac{2}{3}\times (-3)=2$ …（答）

→閉じる←

(3)
yはxに比例し，x=2のときy=−8である。x=−1のときのyの値を求めなさい。

（栃木県2017年入試問題）

解説やり直す

y=−2 y=−3 y=4 y=6

yがxに比例するとき
y=ax（aは定数）
とおける．
x=2のとき，y=−8であるから
−8=2a
a=−4
このとき
y=−4xと書けるから
x=−1のときy=−4×(−1)=4 …（答）

→閉じる←

【例題２】

yがxに反比例し，x=3のときy=8である。y=6のときのxの値を求めよ。

（山口県2017年入試問題）

（解答）
yがxに反比例するとき
$y=\frac{a}{x}$ （aは定数）
とおける．
x=3のとき，y=8であるから
$8=\frac{a}{3}$
a=24
このとき
$y=\frac{24}{x}$
になるから，y=6のとき
$6=\frac{24}{x}$
6x=24
x=4…（答）

【問題２】

(1)
yはxに反比例し，x=6のときy=−12である。x=−9のときのyの値を答えなさい。

（新潟県2015年入試問題）

解説やり直す

y=4 y=8 y=−4 y=−8

yがxに反比例するとき
$y=\frac{a}{x}$ （aは定数）
とおける．
x=6のとき，y=−12であるから
$-12=\frac{a}{6}$
a=−72
このとき
$y=-\frac{72}{x}$
になるから，x=−9のとき
$y=-\frac{72}{-9}=8$ …（答）

→閉じる←

(2)
yはxに反比例し，x=−3のときy=−5です。このとき，yをxで表しなさい。

（岩手県2015年入試問題）

解説やり直す

$y=\frac{5}{3}x$ $y=\frac{3}{5x}$ $y=\frac{x}{15}$ $y=\frac{15}{x}$

yがxに反比例するとき
$y=\frac{a}{x}$ （aは定数）
とおける．
x=−3のとき，y=−5であるから
$-5=\frac{a}{-3}$
a=15
このとき
$y=\frac{15}{x}$ …（答）

→閉じる←

(3)
yはxに反比例し，x=4のときy=−12である。このとき，yをxで表しなさい。

（秋田県2015年入試問題）

解説やり直す

$y=-\frac{3}{x}$ $y=\frac{3}{x}$ $y=-\frac{48}{x}$ $y=\frac{48}{x}$

yがxに反比例するとき
$y=\frac{a}{x}$ （aは定数）
とおける．
x=4のとき，y=−12であるから
$-12=\frac{a}{4}$
a=−48
このとき
$y=-\frac{48}{x}$ …（答）

→閉じる←

(4)
yはxに反比例し，x=4のときy=−4である。x=2のときのyの値を求めなさい。

（兵庫県2015年入試問題）

解説やり直す

−8 −4 2 8

yがxに反比例するとき
$y=\frac{a}{x}$ （aは定数）
とおける．
x=4のとき，y=−4であるから
$-4=\frac{a}{4}$
a=−16
このとき
$y=-\frac{16}{x}$
x=2のとき
$y=-\frac{16}{2}=-8$ …（答）

→閉じる←

(5)
yはxに反比例し，x=−5のときy=6である。このときの比例定数を求めなさい。

（島根県2015年入試問題）

解説やり直す

$-\frac{6}{5}$ $-\frac{5}{6}$ $-\frac{1}{30}$ $-30$

yがxに反比例するとき
$y=\frac{a}{x}$ （aは比例定数）
とおける．
x=−5のとき，y=6であるから
$6=\frac{a}{-5}$
a=−30 …（答）

→閉じる←

【例題３】

反比例の関係 $y=-\frac{12}{x}$ で，xの値が1から3まで変わるときの変化の割合を求めなさい。

【変化の割合】
xの値がx1からx2に変わるとき
yの値がy1からy2に変わるときの変化の割合は
xの増加量x2−x1に対する yの増加量y2−y1の割合
$\frac{y_2-y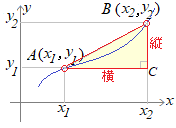_1}{x_2-x_1}$
で定義されます．

初めの点をA(x1, y1)，後の点をB(x2, y2)とし，グラフを上図のように階段状に切ったとき，xの増加量は「横」の長さ，yの増加量は「縦」の長さになります．
　したがって，（変化の割合）＝（縦）÷（横）は，線分ABの傾きを表しています．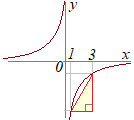

（解答）
$y=-\frac{12}{x}$
において，x=1のときy=−12，x=3のときy=−4だから，変化の割合は
$\frac{(-4)-(-12)}{3-1}=\frac{8}{2}=4$ …（答）

【問題３】

(1)
反比例の関係 $y=\frac{6}{x}$ で，xの値が1から3まで変わるときの変化の割合を求めなさい。

（鳥取県2017年入試問題）

解説やり直す

−4 −2 2 4

x	1	→	3
y	6	→	2

※ゆっくりとこのような表を書くとよいでしょう．

$y=\frac{6}{x}$ において，x=1のときy=6，
x=3のときy=2だから，変化の割合は
$\frac{2-6}{3-1}=\frac{-4}{2}=-2$ …（答）

→閉じる←

(2)
反比例 $y=\frac{6}{x}$ の，xの変域が2≦x≦3のときのyの変域と，反比例 $y=\frac{a}{x}$ の，xの変域が−6≦x≦−4のときのyの変域が一致するとき，aの値を求めなさい。
　ただし，a<0とします。

（宮城県2017年入試問題）

解説やり直す

a=6 a=8 a=−6 a=−12

$y=\frac{6}{x}$ について

x	2	→	3
y	3	→	2

$y=\frac{a}{x}$ について

x	−6	→	−4
y	$\frac{a}{-6}$	→	$\frac{a}{-4}$

※変域は結果が一致すれば等しいというので，y:2→3とy:3→2でも，変域は等しいということに注意

$\frac{a}{-6}=3,\hspace{5}\frac{a}{-4}=2$ …(A)
$\frac{a}{-6}=2,\hspace{5}\frac{a}{-4}=3$ …(B)
(A)は解なし．(B)からa=−12 …（答）

→閉じる←

(3)
関数 $y=-\frac{8}{x}$ について，xの変域がb≦x≦8のとき，yの変域は−4≦y≦cである。b, cの値をそれぞれ求めなさい。

（山形県2017年入試問題）

解説やり直す

b=−2, c=−1 b=−2, c=1

b=2, c=−1 b=2, c=1

$-\frac{8}{b}=-4$ よりb=2
$-\frac{8}{8}=c$ よりc=−1 …（答）

→閉じる←

...（PC版）メニューに戻る

笆�縺薙�繧ｵ繧､繝亥�縺ｮGoogle讀懃ｴ｢笆�

笆ｳ縺薙�繝壹�繧ｸ縺ｮ蜈磯�ｭ縺ｫ謌ｻ繧銀無縲� 繧｢繝ｳ繧ｱ繝ｼ繝磯∽ｿ｡縲�
… 縺薙�繧｢繝ｳ繧ｱ繝ｼ繝医�謨呎攝謾ｹ蝟��蜿り�↓縺輔○縺ｦ縺�◆縺�縺阪∪縺�

笆�縺薙�鬆√↓縺､縺�※�瑚憶縺�園�梧が縺�園�碁俣驕輔＞縺ｮ謖�遭�後◎縺ｮ莉悶�諢滓Φ縺後≠繧後�騾∽ｿ｡縺励※縺上□縺輔＞��

笳区枚遶�縺ｮ蠖｢繧偵＠縺ｦ縺�ｋ諢滓Φ縺ｯ蜈ｨ驛ｨ隱ｭ縺ｾ縺帙※繧ゅｉ縺｣縺ｦ縺�∪縺呻ｼ�
笳区─諠ｳ縺ｮ蜀�〒�後←縺ｮ蝠城｡後′縺ｩ縺�〒縺ゅ▲縺溘°繧呈ｭ｣遒ｺ縺ｪ譁�ｫ�縺ｧ莨昴∴縺ｦ縺�◆縺�縺�◆謾ｹ蝟�ｦ∵悍縺ｫ蟇ｾ縺励※縺ｯ�悟庄閭ｽ縺ｪ髯舌ｊ蟇ｾ蠢懊☆繧九ｈ縺�↓縺励※縺�∪縺呻ｼ趣ｼ遺ｻ縺ｪ縺奇ｼ梧判謦�噪縺ｪ譁�ｫ�縺ｫ縺ｪ縺｣縺ｦ縺�ｋ蝣ｴ蜷医��後◎繧後ｒ蜈ｬ髢九☆繧九→遲��□縺代〒縺ｪ縺剰ｪｭ閠�ｂ隱ｭ繧縺薙→縺ｫ縺ｪ繧翫∪縺吶�縺ｧ�梧治逕ｨ縺励∪縺帙ｓ�趣ｼ�

雉ｪ蝠上↓蟇ｾ縺吶ｋ蝗樒ｭ斐�荳ｭ蟄ｦ迚医�縺薙�鬆��碁ｫ俶�｡迚医�縺薙�鬆�縺ｫ縺ゅｊ縺ｾ縺�