|
【問題1】
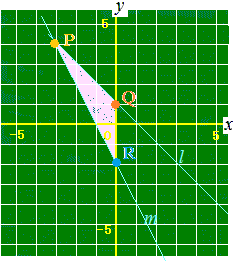
(答案)次の2直線l, mとy軸とで囲まれた三角形の面積を求めなさい. y=−x+5 …(m) 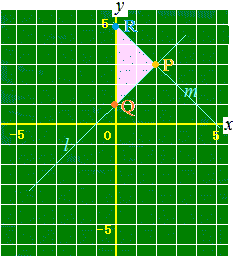 −2 −1 0 1 2 3
y=x+1 …(l)とy軸x=0の交点のy座標を求めるにはy=x+1 …(l)にx=0を代入します.
直線mとy軸との交点Rのy座標は解説
y=0+1=1 したがって,交点のy座標は1になります. 参考までに,交点の座標は(0, 1)です. 0 1 2 3 4 5
y=−x+5 …(m)とy軸x=0の交点のy座標を求めるにはy=−x+5 …(m)にx=0を代入します.
直線lとmの交点Pの座標は解説
y=0+5=5 したがって,交点のy座標は5になります. 参考までに,交点の座標は(0, 5)です. (2, 2) (2, 3) (3, 2) (3, 3)
y=x+1 …(l)とy=−x+5 …(m)の交点の座標を求めるには,
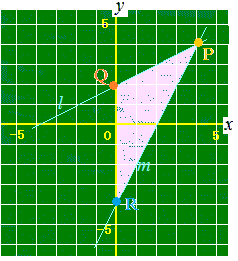
△PQRの面積を求めるときに,y軸上の線分QRを底辺とし,y軸から点Pまでの距離を高さhと考えると
線分QRの長さは解説
1) はじめにyを消去してx座標を求めます. x+1=−x+5 2x=4 x=2 2) 次に,この値を(l)に代入してx座標を求めます. y=2+1=35 したがって,交点の座標は(2, 3)になります. 1 2 3 4 5
Qのy座標は1で,Rのy座標は5だから,大きい方から小さい方を引いて
△PQRの高さhは点Pのx座標(の絶対値)だからQR=5−1=4 解説 1 2 3 4 5
P(2, 3)のx座標は2だから△PQRの高さhは2
△PQRの面積を底辺×高さ÷2,すなわち |
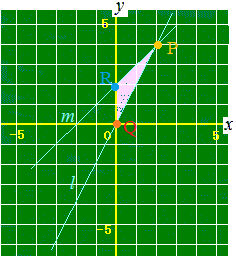
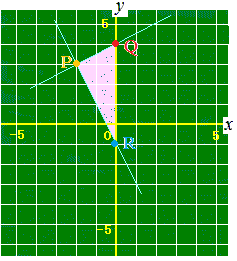
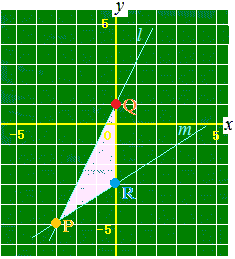
 (
( (
(