|
== 二等辺三角形の角 ==
【重要性質】
右図1の三角形ABCがAB=AC の二等辺三角形ならば ∠ABC=∠ACB が成り立ちます. この性質と三角形の内角の和が180°になるという性質を使うと,二等辺三角形の3つの角のうち1つの角が分かれば,残りの角が求められます. 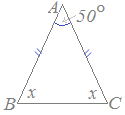 【例1】…頂角が与えられている問題… 【例1】…頂角が与えられている問題…右図の三角形ABCが AB=AC の二等辺三角形ならば ∠ABC=∠ACB が成り立ちます. そこで「三角形の内角の和が180°になる」という性質を使うと 50°+2x=180° 2x=130° x=65° となって,∠ABC=∠ACB=65°が求まります.
上の解説は方程式を解く方法で行いましたが,方程式が苦手な人は,算数で考えてもかまいません.
全部で180°のうち,頂角が50°だから,残りは130° これを2で割ると65° |
図1 ∠Aの二等分線を引くと,左右の三角形が(二辺とその間の角がそれぞれ等しいことにより)合同となって,両底角が等しいことが示されます. 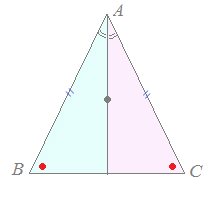
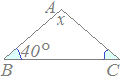 【例2】…底角が与えられている問題… 【例2】…底角が与えられている問題…右図の三角形ABCが AB=AC の二等辺三角形ならば ∠ABC=∠ACB が成り立ちます. そこで「三角形の内角の和が180°になる」という性質を使うと x+2×40°=180° x=180°−80° x=100° となって,∠BAC=100°が求まります. |
|
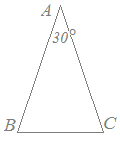
問1次の図においてAB=ACのとき,∠ABCの大きさを求めてください.
 採点するやり直すHELP
採点するやり直すHELP30°+∠ABC×2=180° ∠ABC×2=150° ∠ABC=75°
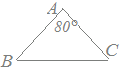
問2次の図においてAB=ACのとき,∠ABCの大きさを求めてください.
 採点するやり直すHELP
採点するやり直すHELP80°+∠ABC×2=180° ∠ABC×2=100° ∠ABC=50° |
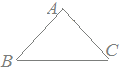
問3次の図においてAB=AC,∠ABC=35°のとき,∠BACの大きさを求めてください.
 採点するやり直すHELP
採点するやり直すHELP∠BAC+35°×2=180° ∠BAC=180°−70° ∠BAC=110°
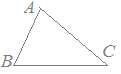
問4次の図においてBC=AC,∠ABC=70°のとき,∠BCAの大きさを求めてください.
 採点するやり直すHELP
採点するやり直すHELP∠BCA+70°×2=180° ∠BCA=180°−140° ∠BCA=40° |
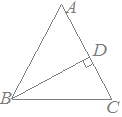 【例3】 【例3】右図の三角形ABCにおいてAB=AC,BD⊥AC,∠A=46°のとき,∠DBCの大きさを求めてください. AB=ACだから∠ABC=∠ACB ∠ABC×2+46°=180° ∠ABC×2=180°−46°=134° ∠ABC=67°=∠ACB △DBCは直角三角形だから ∠DBC=90°−67°=23° |
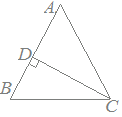
問5次の図においてAB=AC,CD⊥AB,∠DCA=40°のとき,∠CAB,∠ABC,∠BCDの大きさを求めてください.
 採点するやり直すHELP
採点するやり直すHELP△ADCは∠ADC=90°の直角三角形だから ∠CAB=50° △ABCはAB=ACの二等辺三角形だから ∠ABC=(180°−50°)÷2=65° △BDCは∠BDC=90°の直角三角形だから ∠BCD=90°−65°=25°
∠BCD=∠ACB−40°=65°−40°=25°としてもよい.
|
|
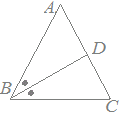
問6次の図においてAB=AC,BDは∠ABCの二等分線,∠DAB=40°のとき,∠CDBの大きさを求めてください.
 採点するやり直すHELP
採点するやり直すHELP△ABCはAB=ACの二等辺三角形だから ∠ABC=(180°−40°)÷2=70° BDは∠ABCの二等分線だから ∠CBD=35° △BDCの内角の和は180°だから ∠CDB=180°−70°−35°=75° |
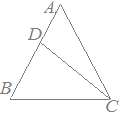
問7次の図においてAB=AC,BC=DC,∠BAC=48°のとき,∠DCAの大きさを求めてください.
 採点するやり直すHELP
採点するやり直すHELP△ABCはAB=ACの二等辺三角形だから ∠ABC=(180°−48°)÷2=66° △BCDはBC=DCの二等辺三角形だから ∠BDC=66° ∠BCD=48° ∠DCA=66°−48°=18° |
|
問8次の図においてAB=AC,BC=DC,∠ACD=15°のとき,∠BACの大きさを求めてください.(やや難)
 採点するやり直すHELP
採点するやり直すHELP∠BAC=x°とおくと △ADCの外角の性質から ∠BDC=x+15° △BCDはBC=DCの二等辺三角形だから ∠DBC=x+15° △ABCはAB=ACの二等辺三角形だから ∠BCA=x+15°,(∠BCD=x) △ABCの内角の和は180°でなければならないから x+(x+15)+(x+15)=180° 3x+30°=180° 3x=150° x=50° |
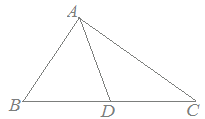
問9次の図においてAB=AD=DC,∠DCA=28°のとき,∠BADの大きさを求めてください.
 採点するやり直すHELP
採点するやり直すHELPAD=DCだから ∠CAD=28° △CDAの外角の性質から ∠BDA=28°+28°=56°
∠ACD=180°−(28°+28°)=124°
△ABDはAB=ADの二等辺三角形だから∠BDA=180°−124°=56° としてもよい. ∠ABD=56° △ABDの内角の和は180°だから ∠BAD=180°−56°×2=68° |
|
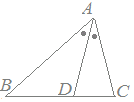
問10次の図においてAD=AC,ADは∠BACの二等分線,∠ABC=30°のとき,∠ACDの大きさを求めてください.
 採点するやり直すHELP
採点するやり直すHELP∠ACD=xとおくと △ADCはAD=ACの二等辺三角形だから ∠ADC=x △ADCの内角の和は180°だから ∠DAC=180°−2x ∠DAC=∠BADだから ∠BAD=180°−2x △ABCの内角の和は180°でなければならないから 30°+x+(360°−4x)=180° −3x=−210° x=70° |
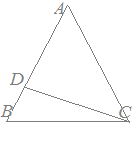
問11次の図においてAB=AC,DA=DC,∠BCD=27°のとき,次の角度の大きさを求めてください.
 採点するやり直すHELP
採点するやり直すHELP∠BAC=xとおくと DA=DCだから ∠DCA=x ∠ACB=x+27° AB=ACだから ∠ABC=x+27° △ABCの内角の和は180°だから x+(x+27°)+(x+27°)=180° 3x=126° x=42° ゆえに ∠BAC=42° ∠ABC=42°+27°=69° |