■連立方程式とグラフ
≪はじめに≫
○ 「連立方程式の解」は数式的に表されるものですが，これは「２直線の交点」という図形的な性質と対応しています．
○ また，この頁で，直線のグラフを考えるときにx軸との交点，y軸との交点をもとにして考える練習をします．（特に，y軸との交点は中学校では切片と呼ばれます．）
■解説
連立方程式
の解x=3, y=4は座標の形では(3, 4)と書くことができます．
連立方程式(1)(2)の解は，２つの方程式(1)(2)を両方とも満たすものですが，これはグラフで考えれば両方の直線上にある点ということになります．
したがって，連立方程式の解は２直線の交点の座標になります．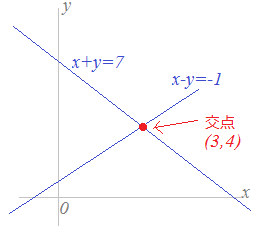
|
※それぞれの直線は「傾きと切片を指定する方法」「２点を指定する方法」などによって定めることができます．
この頁では，それぞれの直線を画面上で表すために【y軸との交点】と【x軸との交点】の２つの点を指定する方法を使います．
【y軸との交点】
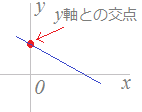y軸を表す直線の方程式は x=0です．
⇒ y軸との交点の座標を求めるためには， x=0を代入して y座標を求めます．
【例】
直線 3x+4y=24と y軸との交点を求めるには，
x=0を代入→ 4y=24→ y=6だから交点の座標は (0, 6)
【x軸との交点】
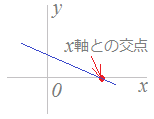x軸を表す直線の方程式は y=0です．
⇒ x軸との交点の座標を求めるためには， y=0を代入して x座標を求めます．
【例】
直線 3x+4y=24と x軸との交点を求めるには，
y=0を代入→ 3x=24→ x=8だから交点の座標は (8, 0)
|
