|
現在地と前後の項目 *** 基本 ***/平方根と√/紙の数学/平方根の近似値 /*** 計算練習 ***/平方根の変形(単独)/平方根の変形(積)/平方根の変形(和差)/平方根の変形(展開)/分母に根号のない形1/分母に根号のない形2/分母に根号のない形3/(徹底練習)２乗,平方根/(徹底練習)根号計算/平方根の計算（答案付き∞）/*** 大小比較 ***/平方根の大小比較1/平方根の大小比較2/平方根の大小比較3/２乗比較/*** 応用問題 ***/試験問題1/試験問題2/試験問題3/試験問題4/試験問題5/試験問題6/平方根→整数ｎ/平方根と式の値/平方根.式の値(入試問題)/平方根.整数(入試問題)/ そもそも
【分母に根号がない形とは】
（解説）【例１】 この数字のだいたいの大きさを求めるために， のように「小数点を移動」して割り算を始めようとしても， これに対して のように前から順に必要な桁数だけ求めることができます． |
【例２】 文字式で
これと同様に
のような形をしていると， の形になっていると と簡単にすることができます． ※このように，さまざまな計算の中に ※分母に根号がない形に変形すると，分子に根号が登場するのが普通ですが，「分子に」根号があるのは「横に」根号があるのと同じで，よい形なのです．
「分母に根号がない形」あるいは「分母に根号を含まない形」に変形することを，高校では「分母の有理化」といいますが，この用語は中学校の教科書には出ていないようです．（高校でもう一度習います）．
|
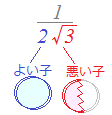⇒「初めに」分母と分子に２も一緒に掛けてしまって，「最後に」２で約分するのなら，無駄な作業を２回行っていることになります．初めから２は掛けないようにすべきです．