|
現在地と前後の項目 *** 基本 ***/三平方の定理1/三平方の定理2/三平方の定理(徹底復習)/*** 距離 ***/2点間の距離1/2点間の距離2/2点間の距離3/震源地/*** 逆の問題 ***/三平方の定理の逆/*** 融合問題 ***/融合問題/問題以上,答以下/展開図形/回転図形1/回転図形2/円と三平方の定理/*** よく出る応用 ***/三角形２個の問題1/三角形２個の問題2/三角形２個の問題3/特別な形の三角形1/特別な形の三角形2/三辺→高さ/*** 空間図形 ***/空間図形と三平方の定理1/空間図形と三平方の定理2/立体の体積，表面積/立体の体積（入試問題）/立体の表面積.展開図（入試問題）/
【三平方の定理】
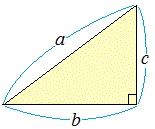
○三平方の定理を使えば，直角三角形の２辺の長さが分かれば残りの１辺の長さが求められる．右図のような直角三角形については
b2+c2=a2
が成り立つ．
たとえば右図では，
b , c が分かっていれば a が求められる．
a , c が分かっていれば b が求められる． a , b が分かっていれば c が求められる． |
|
|
|
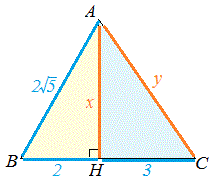
例1 右図で黄色の三角形について三平方の定理を使うとAHの長さが求めることができ，
さらに求めたAHの長さとCHの長さを使って青色の三角形について三平方の定理を使うと辺ACの長さを求めることができる．
22+x2=(2
 √5)2
4+x2=20
x2=16
x=4 (>0)
さらに 42+32=y2
y2=25
y=5 (>0)
|
 |
|
|
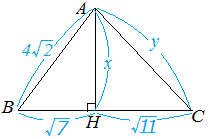
問題１ 右図において x , y の長さを求めなさい．
|
( √7)2+x2=(4√2)2
7+x2=32
x2=25
x=5 (>0) ( √11)2+52=y2
y2=36
y=6 (>0) |
|
|
問題２ 右図において CD の長さ x を求めなさい．
|
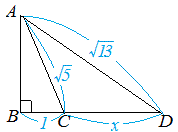直角三角形ABC について三平方の定理を適用すると
12+AB2=( √5)2
AB2=4
AB=2 (>0)
直角三角形ABD について三平方の定理を適用すると
22+(x+1)2=( √13)2
(x+1)2=9
x+1=3 (>0) x=2 |
|
|
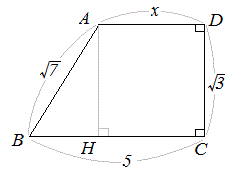
例2 長方形の向かい合う辺の長さは等しいので，右図で AH=DC になる．
このAH の長さとAB の長さから三角形ABH について三平方の定理を使うと辺BH が求まり，HC，AD の長さが分かる．
AH=DC=
△ABH に三平方の定理を適用すると
√3
(
√3)2+BH2=(√7)2
3+BH2=7
BH2=4
したがって
BH=2 (>0)
CH=3
x=3
|
 |
|
|
問題３ 右図において CD の長さ x を求めなさい．
|
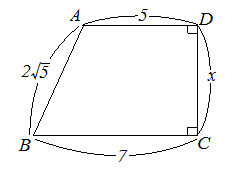A からBC に垂線AH を引くと
HC=AD=5 , BH=2
直角三角形ABH に三平方の定理を適用すると
BH2+AH2=AB2
22+x2=(2 √5)24+x2=20 x2=16 x=4 (>0) |
|
|
直角三角形ABC に三平方の定理を適用すると
202+152=AC2
△ABC と△ADB は直角三角形で１つの角A が共通だから「２つの角がそれぞれ等しい」．したがって△ABC∽△ADBAC2=400+225=625=252 AC=25 (>0) 相似三角形の２組の辺の比は等しいから
AC:CB=AB:x
25:20=15:x 25x=300 x=12 （別解） この問題については，△ABC の面積S を２通りの方法で表して，それらが等しいことからx を求める方法もある．（１つの方法で行き詰ったときのために，別ルートも覚えておくと助かることがある．）
AB · BC / 2 = S = AC · x / 2
AB · BC = 2S = AC · x 15 · 20 = 2S = 25 · x x=12 |
 |
|
|
問題４ 右図において BD の長さ x を求めなさい．
|
△ABC に三平方の定理を適用すると
AB2+BC2=AC2
△ACB∽△ABD だから
( √5)2+BC2=525+BC2=25 BC2=20 BC=2 √5 (>0)
AC:CB=AB:x
5:2 √5=√5:x5x=10 x=2 |
|
|
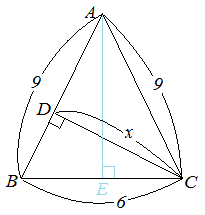
例4 二等辺三角形では，頂点から底辺に引いた垂線は底辺を二等分するので，直角三角形を使って高さを求めることができる．
△ABC はAB=AC の二等辺三角形だから，A からBC に垂線BE をひくとAE⊥BC，BE=EC=3 になる．さらに相似図形の性質を使えば，右図 DC の長さも求められる． 直角三角形ABE に三平方の定理を適用すると
32+AE2=92
△ABE と△BCD は直角三角形で１つの角B が共通だから「２つの角がそれぞれ等しい」．したがって△ABE∽△BCDAE2=72 AE=6 √2 (>0)
相似三角形の２組の辺の比は等しいから
BA:AE=BC:CD
9:6 √2=6:x9x=36 √2x=4 √2
（別解） △ABC の面積をS とおくと
AE · BC / 2 = S = AB · x / 2
6 √2 · 6 / 2 = 9 · x / 2両辺を２倍して分母をはらうと 36 √2= 9 · xx=4 √2 |
 |
|
|
問題５ 右図の二等辺三角形ABC において頂点 C からAB にひいた垂線の長さ x を求めなさい．
|
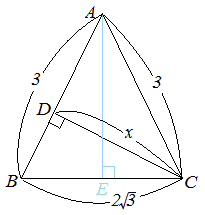△ABC は二等辺三角形だからAE⊥BC，BE=EC=√3 になる．△ABE に三平方の定理を適用すると
(
△ABE∽△BCD だから
√3)2+AE2=323+AE2=9 AE2=6 AE= √6 (>0)
BA:AE=BC:x
3: √6=2√3:x3x= √6 · 2√3 = 6√2x=2 √2
|